
Определение направления на местную вертикаль для наноспутника класса CubeSat
…
Инженерный журнал: наука и инновации
# 8·2016 5
( )
сеч
o
2
2
2
2
2
sin
cos
;
kx ky
x
kz
kx
kz
kx
ky
kz
n n t
R
X C
n t
n n
n n n
= +
−
+
+ +
2
2
сеч
2
2
2
sin ;
kx
kz
o
y
kx
ky
kz
R n n
Y C
t
n n n
+
= +
+ +
(8)
( )
сеч
o
2
2
2
2
2
sin
cos
,
kz ky
z
kx
kx
kz
kx
ky
kz
n n t
R
Z C
n t
n n
n n n
= −
+
+
+ +
где
[
]
0; 2 .
∈ π
t
Зная координаты точек окружности и координаты крайних точек
кадра, определим принадлежность точек окружности прямоугольни-
ку кадра. Если точка попадает в кадр, то это означает, что камера ее
видит. Определим попадание произвольной точки окружности
Т
с
координатами
(
)
, ,
x y z
T T T
в прямоугольник с вершинами 1–4 (коор-
динаты вершин известны). Построим векторы из точки
Т
в вершины
прямоугольника. Точка
Т
будет принадлежать прямоугольнику, если
сумма площадей треугольников
Т
12,
Т
23,
Т
34 и
Т
41 равна площади
прямоугольника 1234 (рис. 4).
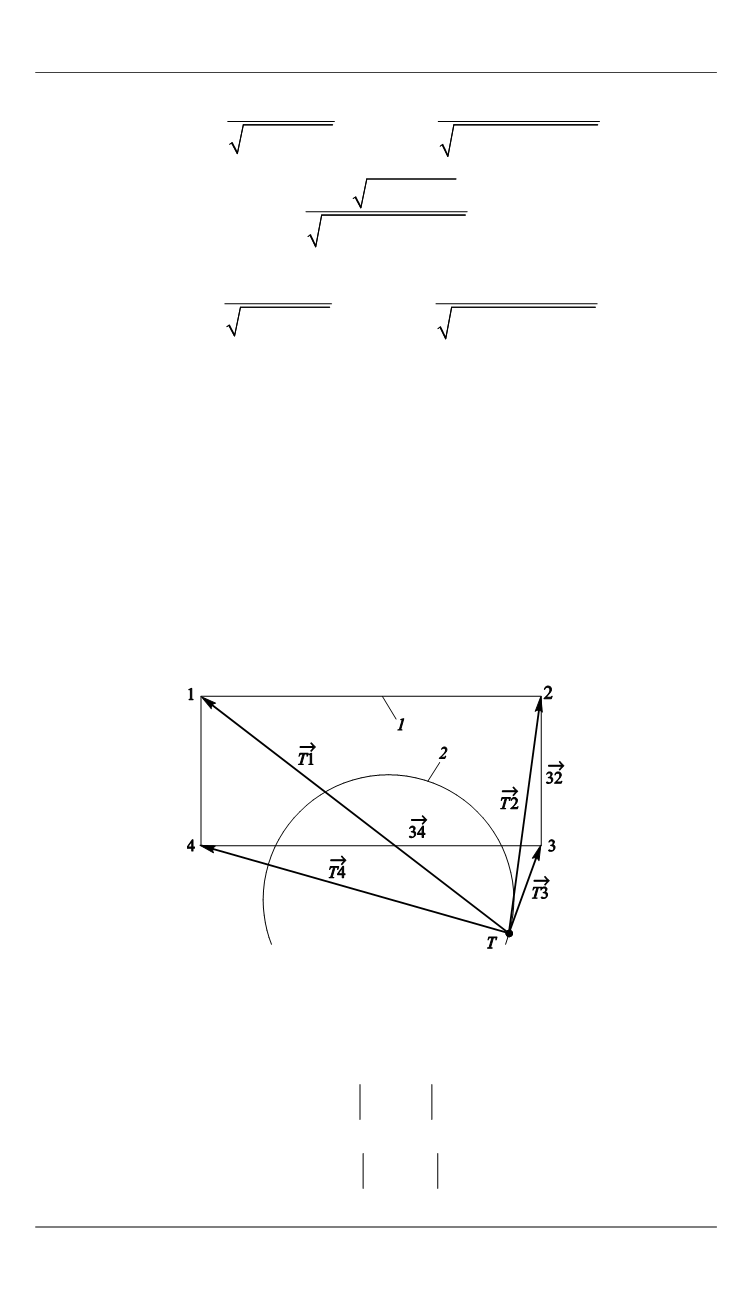
Рис. 4.
К определению принадлежности точки
Т
прямоугольнику кадра:
1
— граница кадра;
2
— дуга горизонта
Площади треугольников определим по следующим формулам:
12
0,5 1 2 ;
Т
S
T T
=
×
(9)
23
0,5 2 3 ;
Т
S
T T
=
×
(10)


















