
А.И. Жакин, А.А. Гримов, А.А. Луценко, В.А. Пиккиев
4
Инженерный журнал: наука и инновации
# 5·2016
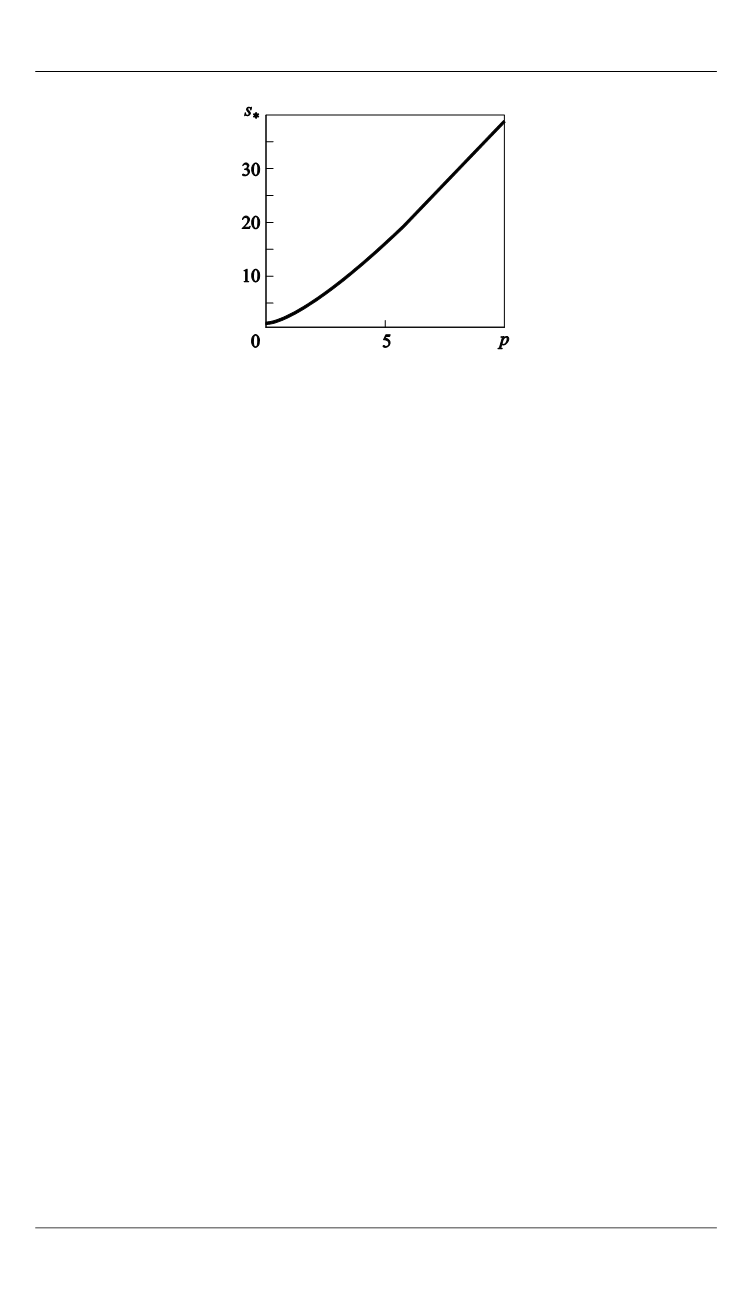
Рис. 2
. График функции
( )
s p
∗
Значения функции
( )
s p
∗
p....................
0,1 0,5 1 1,5 2 2,5 3 3,5 4 5 6 10
s
∗
................... 1,1 1,63 2,53 3,68 5,03 6,54 8,18 9,93 11,78 15,7 19,89 38,47
Из приведенных данных следует, что при
0,3
p
<
корни
s
∗
мож-
но аппроксимировать как
1 / (1 )
s
p p
∗
≈ ( −
, при 1
3
p
≤ ≤
прибли-
женно
2,5
s
p
∗
≈
, при
4
6
p
≤ ≤
выполняется
3
s
p
∗
≈
, что удобно
для оценочных расчетов.
Таким образом, электроны, имеющие начальную координату
0
r
,
будут переходить на круговую орбиту радиуса
r
∗
, определяемого вы-
ражением
2 2
0
/ ( ),
/(2 ),
H
r r s p p v v
∗
∗
∗
=
=
0
.
H H
v
r
= ω
(12)
Отсюда следует, что размер
r
∗
стремится к
0
r
в сильных магнитных
полях, когда для любого
0
r
выполняется условие
1
p
<<
. Наоборот, в
сильных электрических полях, когда при любых
0
r
выполняется
условие
1,
p
>
будет
( ) 2,53
s p
∗
>
, т. е.
r
∗
<
0
r
.
В этом случае начальная радиальная координата электронов
0
r
∗
,
при которой их орбиты будут круговыми с радиусом центрального
электрода
1
,
r R
∗
=
определяется уравнением
2 2
0
1
2
( ) ,
/(2 ),
H
r s p R p v v
∗ ∗ ∗
∗ ∗
=
=
0
.
H H
v
r
∗
∗
= ω
(13)
Причем электроны, которые в начальный момент времени имели ра-
диальные координаты
0 0
,
r r
∗
<
будут поглощаться центральным элек-
тродом (анодом, если пренебречь ударной эмиссией электронов из
анода).
















