
Баллистические аспекты полета КА для изучения дальнего космоса
Инженерный журнал: наука и инновации
# 4·2016 7
Солнца до КА;
Р
— тяга двигателя;
m
— масса КА;
φ
— истинная
аномалия;
с
m
— секундный массовый расход топлива.
Гравитационный маневр.
Для увеличения скорости КА и, сле-
довательно, сокращения времени перелета имеет смысл использовать
гравитационные маневры около естественных небесных тел.
Дополнительное приращение
V
∆
характеристической скорости,
получаемое за счет орбитальной энергии планет или их спутников,
создает возможность существенной экономии ресурсов для полетов на
дальние расстояния. В результате потребуется определять «окна старта»
с Земли, т. е. время, когда необходимые небесные тела будут нахо-
диться в требуемом положении для реализации сценария пролета.
Рассмотрим модель гравитационного маневра. Часто используемый
для расчета гравитационного маневра метод склеенных конических
сечений представляет собой траектории небесного тела пренебрежимо
малой массы (в нашем случае — КА) в кусочно-кеплеровом виде с
изломами в местах проведения гравитационных маневров. Области
проведения маневров (от входа в сферу Хилла второго гравитирующего
тела до выхода из нее) считаются ничтожными по сравнению с
участками кеплерового движения около центрального тела и
заменяются точками склейки [5].
Угол «излома» δ определяется «внутренней геометрией» точки
склейки, исходя из угла раствора «запакованной в этой точке»
пролетной гиперболы относительно пролетного небесного тела.
Модуль вектора скорости КА относительно планеты при этом не
изменяется.
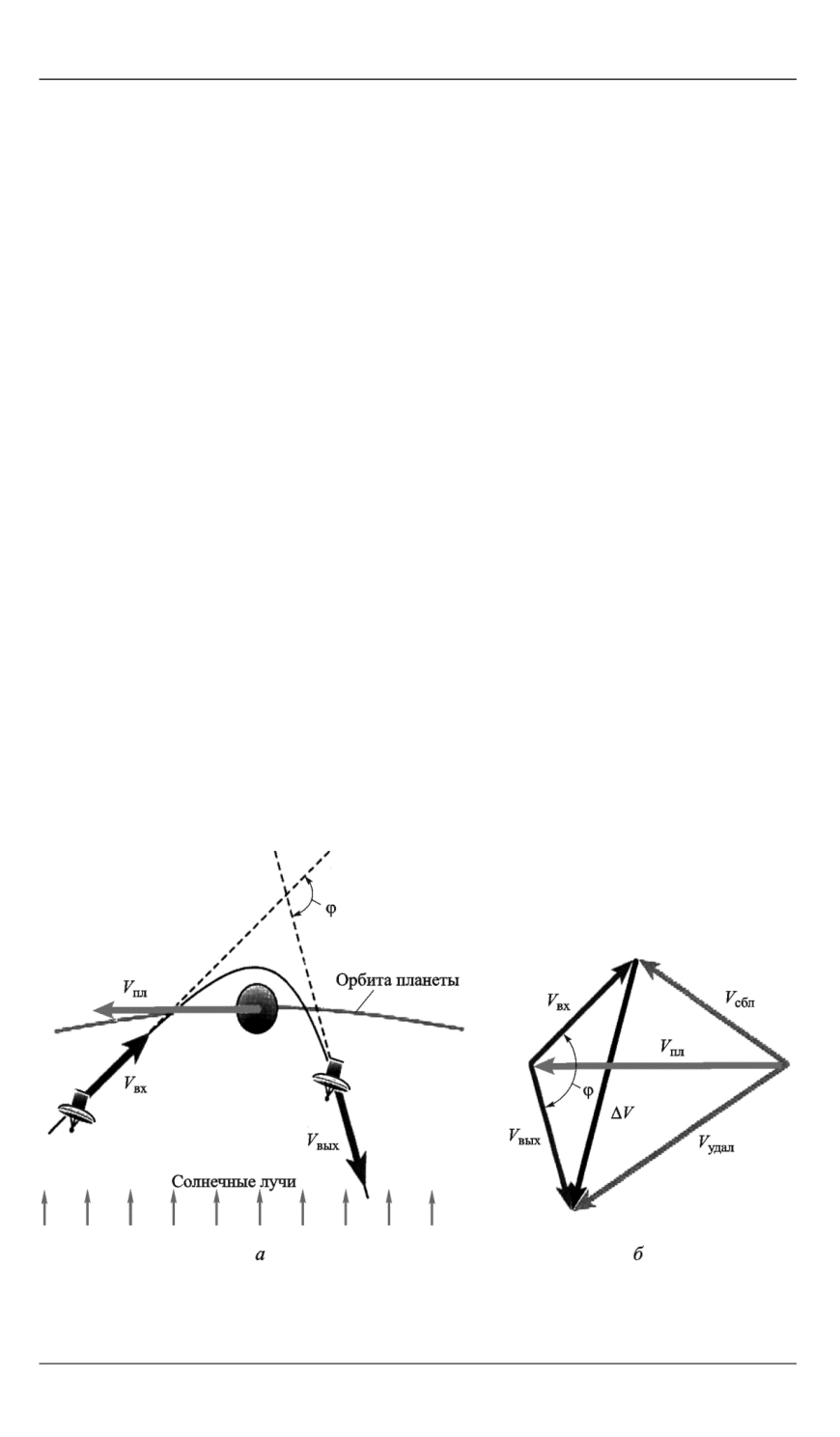
Рис. 3.
Гравитационный маневр (
а
) и диаграмма скоростей (
б
)


















