
Баллистические аспекты полета КА для изучения дальнего космоса
Инженерный журнал: наука и инновации
# 4·2016 3
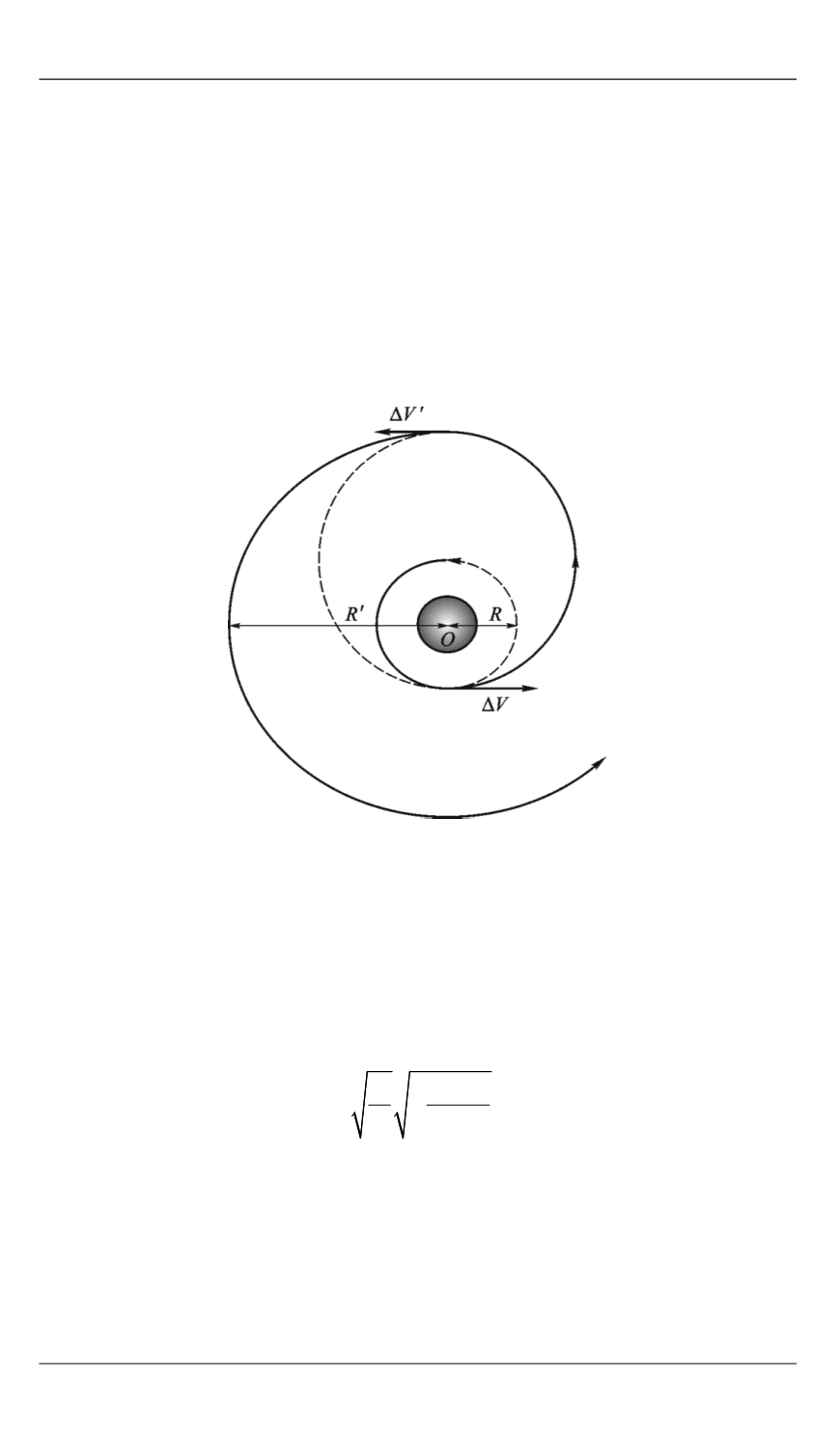
Гомановский переход.
Для выявления важных качественных за-
кономерностей примем упрощенную модель планетных орбит: будем
считать орбиты всех планет круговыми, лежащими в плоскости эк-
липтики. Время работы двигателя на выдачу импульса мало по срав-
нению со временем перелета, а значит, можем положить, что импульс
мгновенный.
Немецкий ученый В. Гоман доказал, что траекторией между
двумя орбитами, на которой затрачивается минимальное количество
топлива, является эллипс, касающийся их в противоположных точках
(рис. 1).
Рис. 1.
Гомановский переход
Примем, что перелет осуществляется по гомановскому переходу,
начальная орбита — орбита Земли вокруг Солнца, а конечная —
орбита вокруг Солнца с радиусом
а
r
= 300 а. е. Минимальное
значение добавочной скорости
вых
V
отлета от Земли рассчитывают
по формуле
а
вых
З
п
п а
μ 2
,
r
V
V
r r r
=
−
+
где μ — гравитационный параметр Земли;
З
V
— скорость Земли;
п
,
r
а
r
— радиус в перигее и апогее соответственно.
Продолжительность
гом
T
перелета по гомановской траектории
вычисляют как половину полного периода обращения искусст-
венной планеты, определяемого по формуле


















