
А.Ю. Егорушкин, В.И. Мкртчян
4
Инженерный журнал: наука и инновации
# 4·2016
элементов и вычислительными ошибками. Компенсация
δ
H
позволяет
свести к минимуму влияние обеих составляющих на определение
координат по формулам (1) — (4).
После определения
δ
H
и
μ
по формулам (9) и (10) их компенсация
проводится на этапе вычисления приращений
Δ
E
,
Δ
N
как
(
)
(
)
Δ 1 μ sin δ ,
E
s H H
= − ∆
−
(11)
(
)
(
)
Δ 1 μ cos
δ .
N
s
H H
= − ∆
−
(12)
В качестве эталонных координат
φ , λ
true true
использовались
координаты приемника GNSS.
Точность оценки погрешностей
δ
H
и
μ
по формулам (9) и (10) тем
выше, чем больше значение
(
) (
)
2
2
Δ
Δ
true
true
E
N
+
. В рассматриваемом
случае для калибровки этих погрешностей был выбран момент времени
1
3431
t
c
=
. Результаты вычислений:
δ
0,177
H
= − °
,
μ 0, 012
=
.
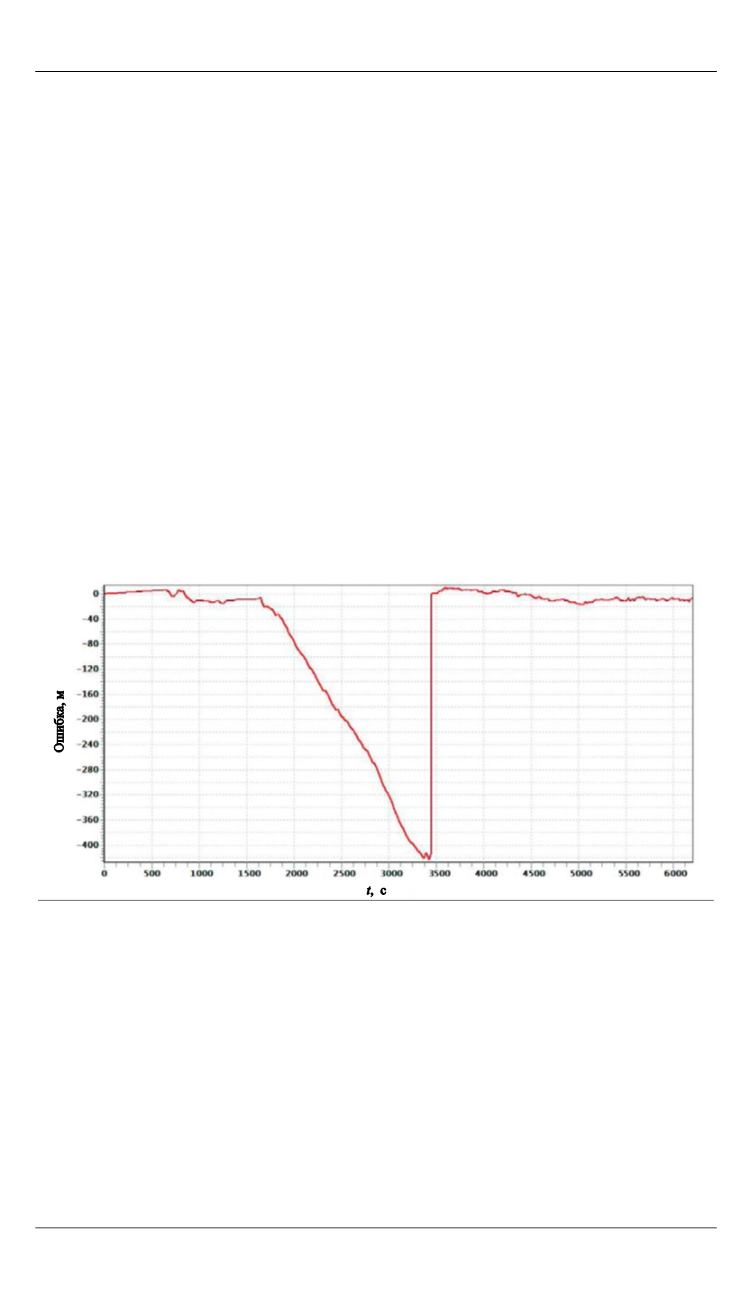
На рис. 1 показана кривая ошибки
δ .
N
До момента времени
1
t
видно нарастание ошибки, обусловленное погрешностями
δ
H
и
μ.
Рис. 1.
Ошибка пройденного пути в северном направлении
В момент времени
1
t
алгоритм производит сброс ошибки
δ ,
N
испо-
льзуя значения
Δ
true
N
. На этом же вычислительном такте определяются
погрешности
δ
H
и
μ,
а начиная со следующего такта и до конца
моделирования они компенсируются в соответствии с формулой (12).
Видно, что после калибровки погрешностей
δ
H
и
μ
остались только
малые девиации ошибки
δ ,
N
обусловленные остаточными нескомпен-
сированными погрешностями и их нестабильностью во времени.
Аналогичные рассуждения справедливы и для ошибки
δ
E
(рис. 2).
















