
О некоторых особенностях поиска оптимального управления …
Инженерный журнал: наука и инновации
# 3
⋅
2016 3
«исходного» существенно сокращает время, затрачиваемое на поиск
приемлемого начального приближения вектора сопряженных
переменных для краевой задачи принципа максимума.
Постановка задачи.
Рассмотрим задачу оптимального прост-
ранственного выведения ОБ с НОО на некомпланарную ей целевую
орбиту в ЦПТЗ. При этом выведение будем анализировать как
переход с орбиты на орбиту: точки старта и окончания выведения
заранее не фиксируют, а получают в результате решения задачи.
Пространственное движение центра масс ОБ с двигателем
большой тяги в ЦПТЗ описываем в абсолютной геоцентрической
экваториальной системе координат (АГЭСК) системой дифферен-
циальных уравнений
3
3
3
μ
cos θ cos γ
,
μ
sin θ cos γ
,
μ sin γ
,
β,
,
,
=
− ≡
=
− ≡
=
− ≡
= −
=
=
=
x
y
z
x
V
y
V
z
V
x
y
P
x
V
f
m
r
P
y
V
f
m
r
P
z
V
f
m r
m
x V
y V
z V
,
z
(1)
где
, ,
x y z
— координаты центра масс ОБ;
, ,
x y z
V V V
— проекции
вектора скорости на соответствующие оси АГЭСК;
,
,
x
y
z
V V V
f f
f
—
проекции вектора ускорения на соответствующие оси АГЭСК;
14
μ 3,986005 10
=
⋅
м
3
/с
2
— гравитационный параметр Земли;
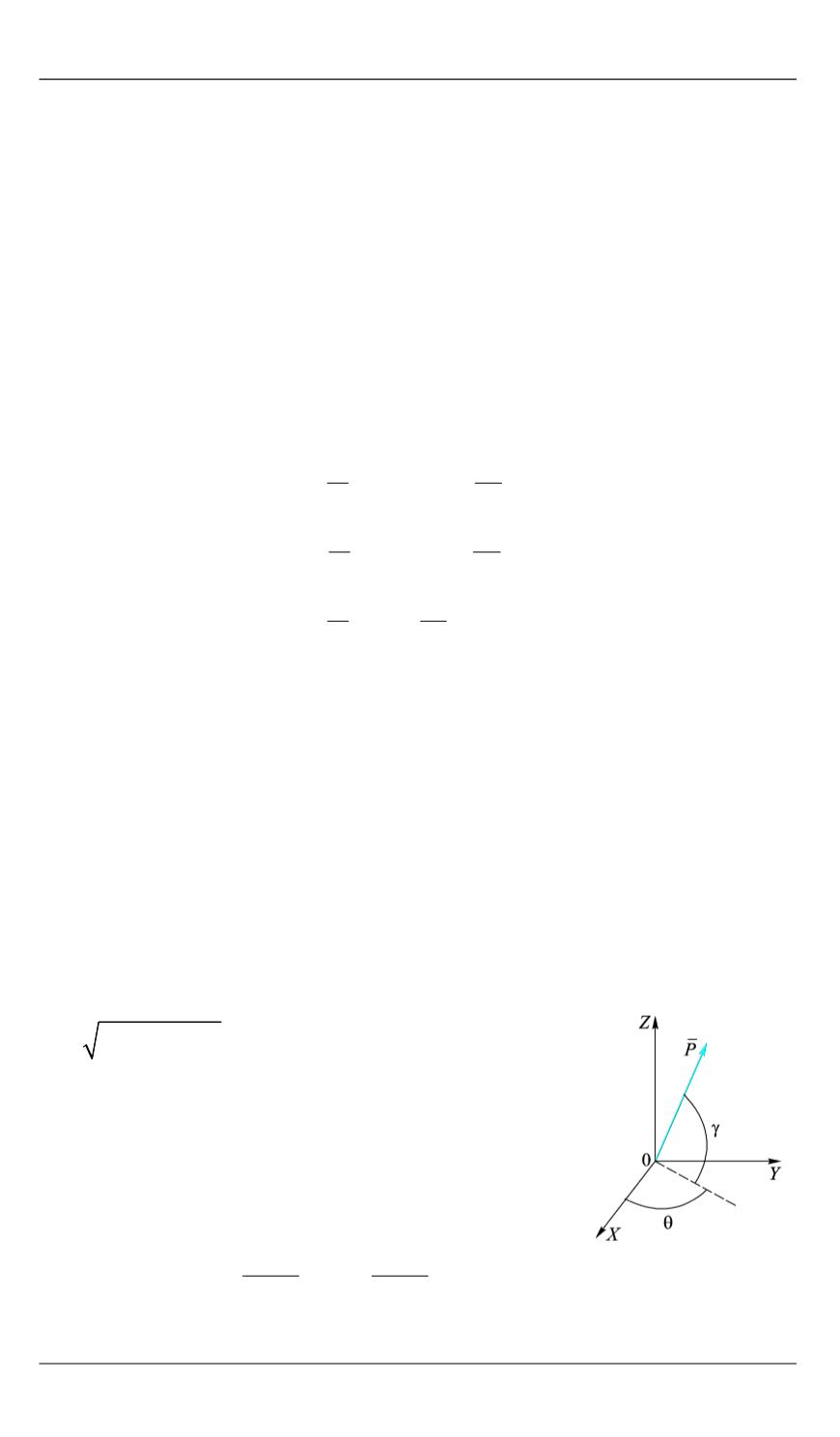
θ, γ
—
углы ориентации вектора тяги (рис. 1);
2 2 2
= + +
r x y z
— модуль радиус-вектора.
Для удобства и унификации расчетов без
привязки к конкретному типу ОБ производят
нормирование массы ОБ (
( )
m t
) и массового
секундного расхода топлива (
β
) относительно
начальной массы ОБ:
0
( )
( )
( )
=
m t
m t
m t
,
0
β β
( )
=
m t
.
Рис. 1.
Ориентация
вектора тяги в АГЭСК


















