
А.Б. Поддоскин
6
В случае чисто упругих столкновений молекул газа друг с другом
1
0.
Z
Если, кроме этого, формально предположить, что коэффи-
циент диффузии внутренней энергии молекул равен нулю, то полу-
чим переход к одноатомному газу [7]. Тогда (7) преобразуется
в выражение для коэффициента барнеттовского скольжения одно-
атомного газа, полученного в приближении кинетической S-модели.
При этом значения параметров
,
0,1, 2 ,
i
i
i
1
,
2
равны:
0
1;
0
0,5182;
1
0, 2787;
1
0,1890;
2
0,8975;
2
0, 0929;
0
1;
0
0,1810;
1
1,1165;
1
0, 0945;
2
0,1794;
2
0, 0060;
1
1, 2560;
2
2,1431.
Используя эти параметры, находим коэффициент барнеттовского
скольжения β
B
= 4,538 (при
q
= 1) — результат совпадает с получен-
ным в приближении S-модели. Отметим, что в теории термофореза [2]
используется коэффициент барнеттовского скольжения
(0)
/
Б B TS
K
(здесь
(0)
TS
K
— коэффициент теплового скольжения газа), числовое
значение которого в этом случае
3,844.
Б
Далее при расчете коэффициента барнеттовского скольжения
многоатомного газа
B
используем формулу Сандлера [11] для ко-
эффициента диффузии
.
r
D
При этом параметр
r
определяем как [7]
2
3
0, 27 0, 44 0, 90
1,32 1
r
Z Z Z
— см. рисунок.
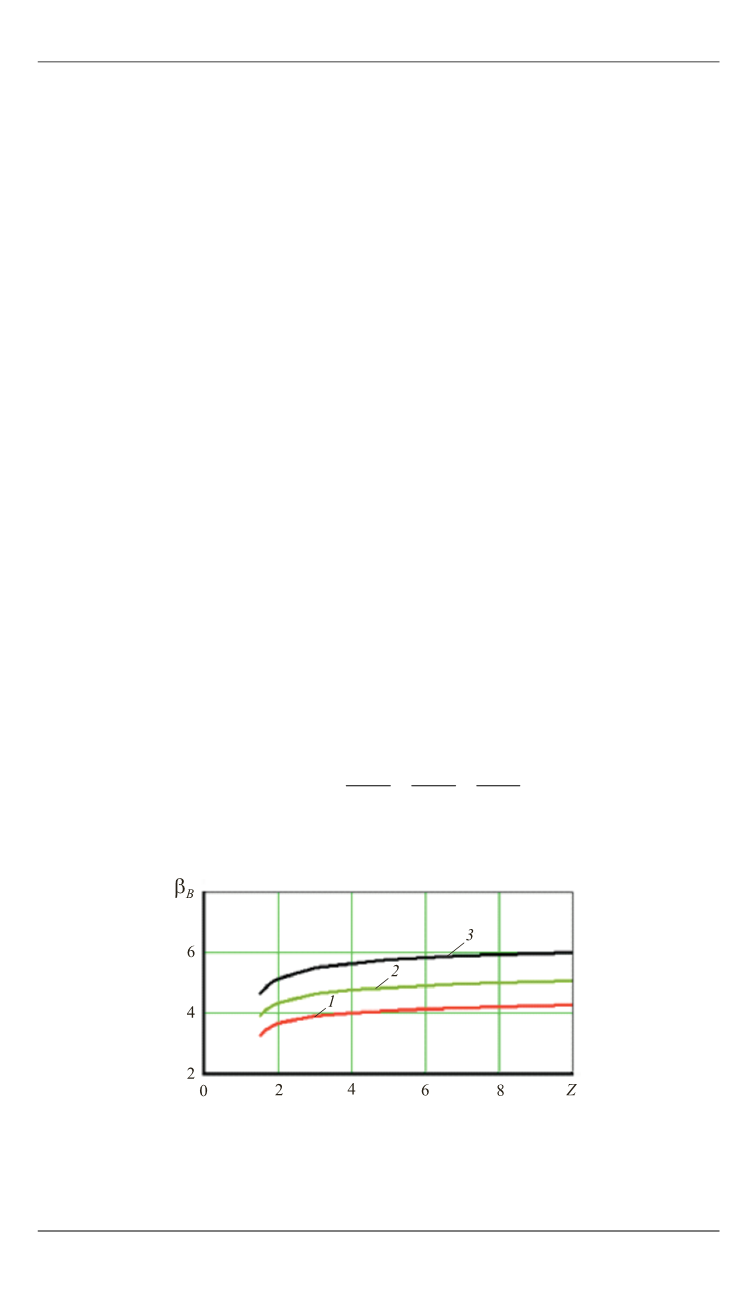
Зависимость коэффициента барнеттовского скольжения
B
от числа неупругих столкновений
Z
:
1
—
q
= 1;
2
—
q
= 0,9;
3
—
q
= 0,8

















