
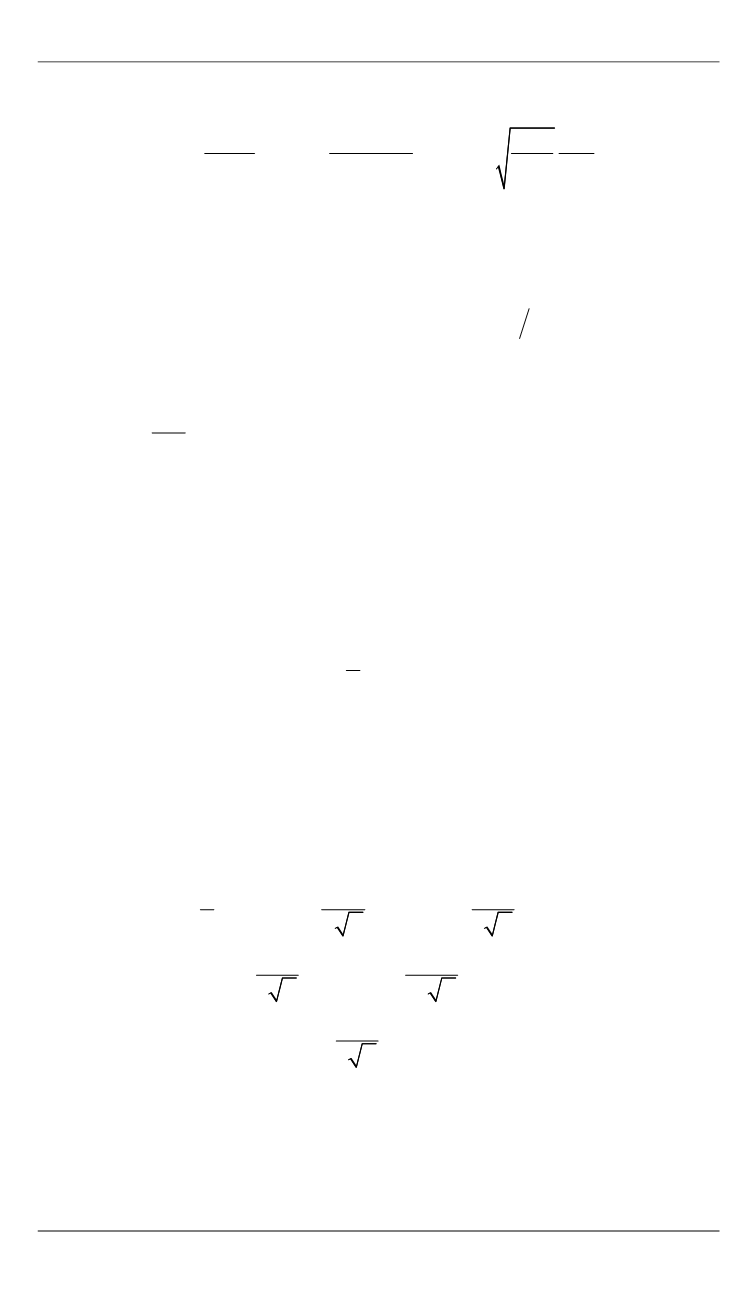
Влияние неупругих столкновений молекул многоатомного газа…
3
d
1
= a
1
b
1
/
2;
d
2
= a
2
b
1
/
2;
0
;
T g = T x
2
0
;
T
T =
T x x
0
.
u m =
x 2kT
Пусть над твердой плоской поверхностью находится многоатомный
газ, в котором создан неоднородный градиент температуры. Направим
ось
ОХ
декартовой системы координат перпендикулярно поверхности,
а ось
OY
вдоль нее. Будем считать, что из компонент тензора напряже-
ний
T
отличной от нуля будет только
2
0
,
xy
T T T x y
=
тогда мо-
дельное кинетическое уравнение (1) для Ф можно записать следующим
образом:
2
2
1
2
0
2
5/2
3/2 ,
t
r
x
y y
y y
y y
dc
= c G c Q c
c Q c
dx
(2)
где
х
0
=
ε
x.
Далее задачу решаем методом полупространственных моментов [7].
Функцию Ф ищем в виде
( )
( )
,
= + + –
где
1 ( )
1 sign ;
2
x
=
c
sign 1
x
c
для
c
x
>
0;
sign –1
x
c
для
c
x
<
0;
2
0
1
2
2
3
( )
( )
5/2 ( )
3 / 2 ( ).
y
x y
y x
y x
= c a x c c a x c c c
a x
c c c
a x
При этом макропараметры газа
G
y
,
Q
t
y
,
Q
r
y
имеют вид:
0 0
1 1
2 2
1
1
1
(
)
(
)
(
);
4
4
8
y
G a a
a a
a a
1 1
2 2
13
1 (
)
(
);
8
16
t
y
Q
a a
a a
3 3
3 (
).
8
r
y
Q
a a
Умножая уравнение (2) последовательно на выражения
2 2
( ) exp(
);
y
c
c c
2 2
( )
exp(
);
y x
c c
c c

















