Управление колебаниями системы маятник-тележка с приводом методом скоростного биградиента

2 / 9

Я.А. Долгов, А.А. Зюзин, А.В. Финошин, Ю.И. Мышляев
2
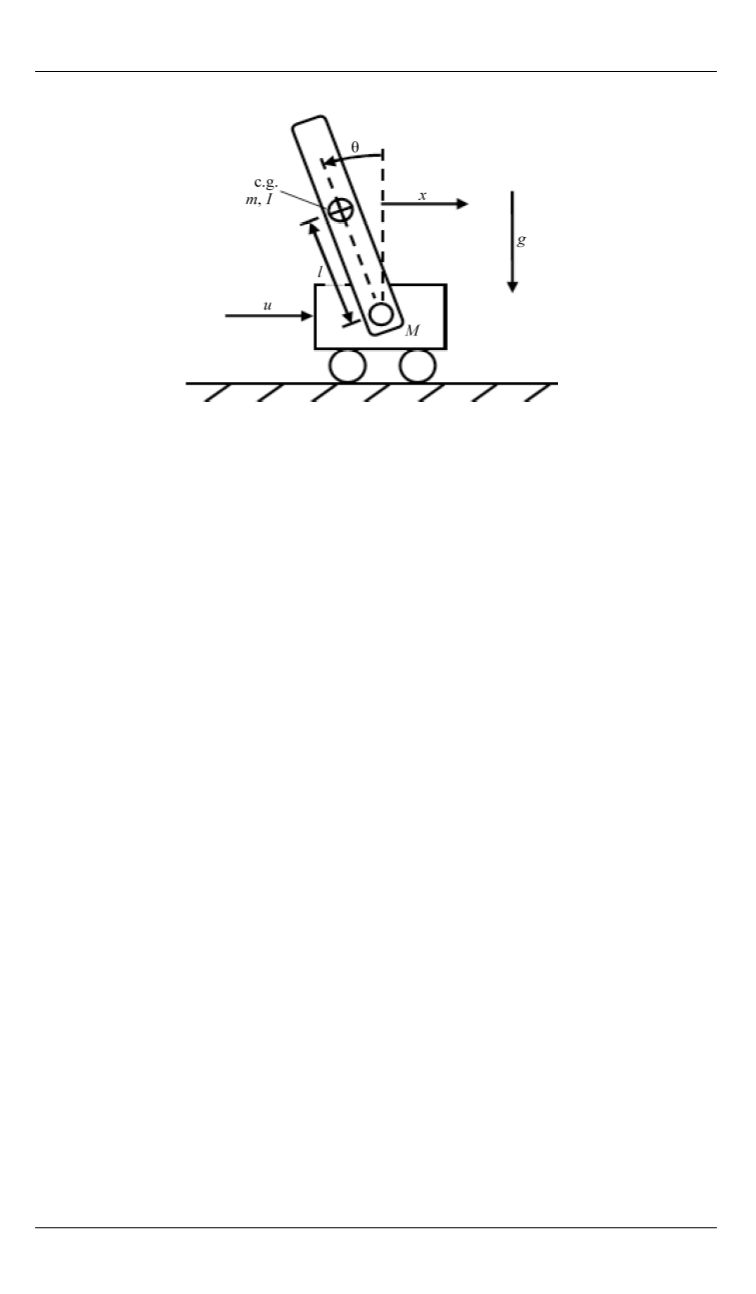
лежке, которая катится свободно по плоской поверхности. Тележка с
маятником имеет две степени свободы.
Уравнение системы в лагранжевой форме:
2
cos 0 sin
cos 0 0
0 1
,
sin 0
M m ml x x ml
ml I ml
f
mgl
           
        
    
      
   
 
   
 
    (1)
где М — масса тележки; m — масса маятника; l — длина маятника;
I — момент инерции маятника; f — управляющая сила.
Уравнение (1) можно записать в матричной форме:
( ) ( , ) ( , ) , H C Bf    q q q q q φ q q (2)
где  T
x   q — вектор обобщенных координат; H — симметрич-
ная положительно определенная матрица масс; C — матрица центро-
стремительных сил и сил Кориолиса;  — вектор потенциальных сил,
B — матрица из единицы и нуля соответствующего размера.
Не умаляя общности, будем считать, что динамика привода опи-
сывается интегратором. Уравнение привода, генерирующего силу,
приводящую тележку в движение, будет следующим:
, f u (3)
где и — управление.
Целью управления (ЦУ) является раскачивание маятника с до-
стижением колебаний заданного уровня энергии
Рис. 1. Тележка с маятником