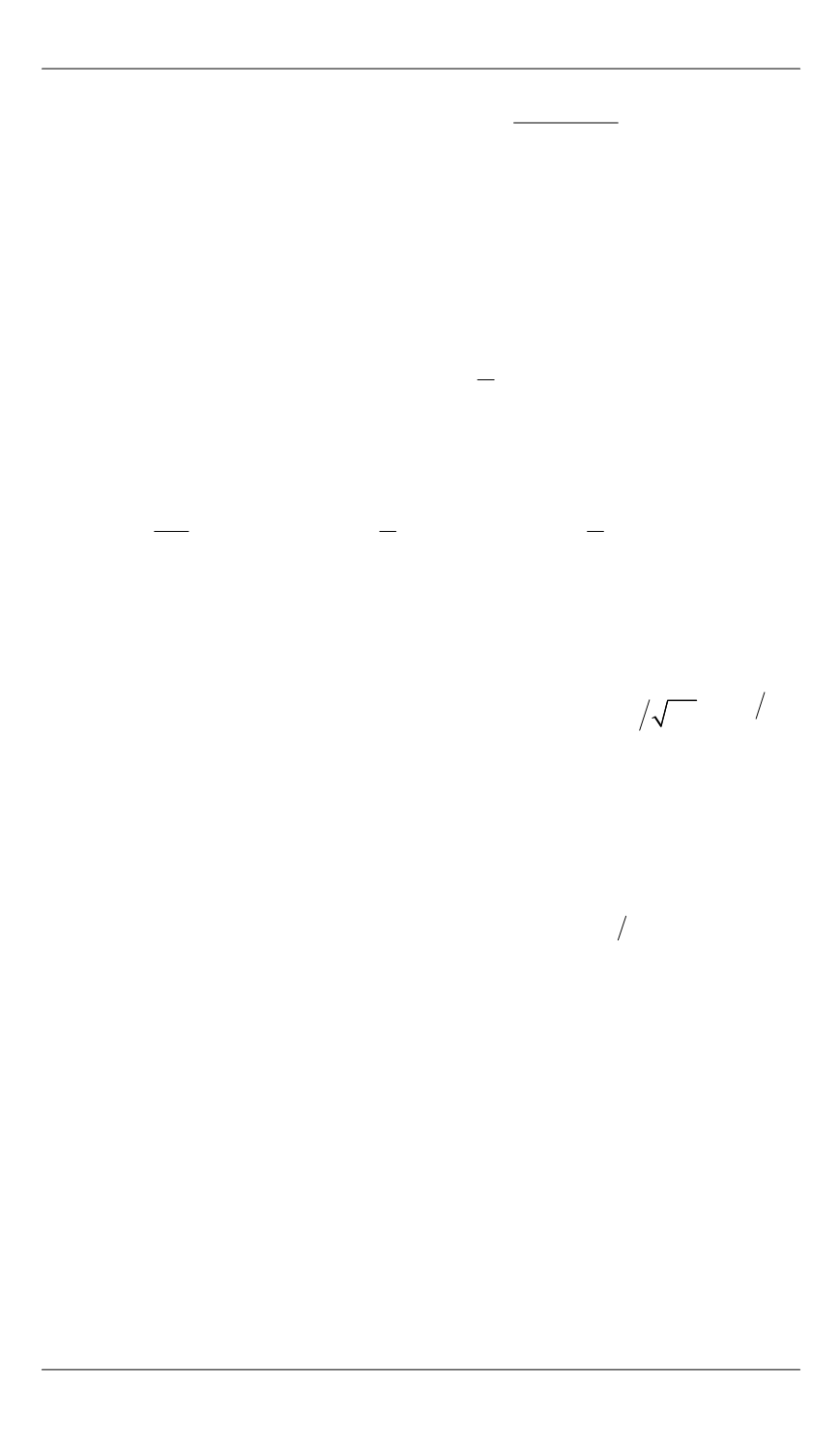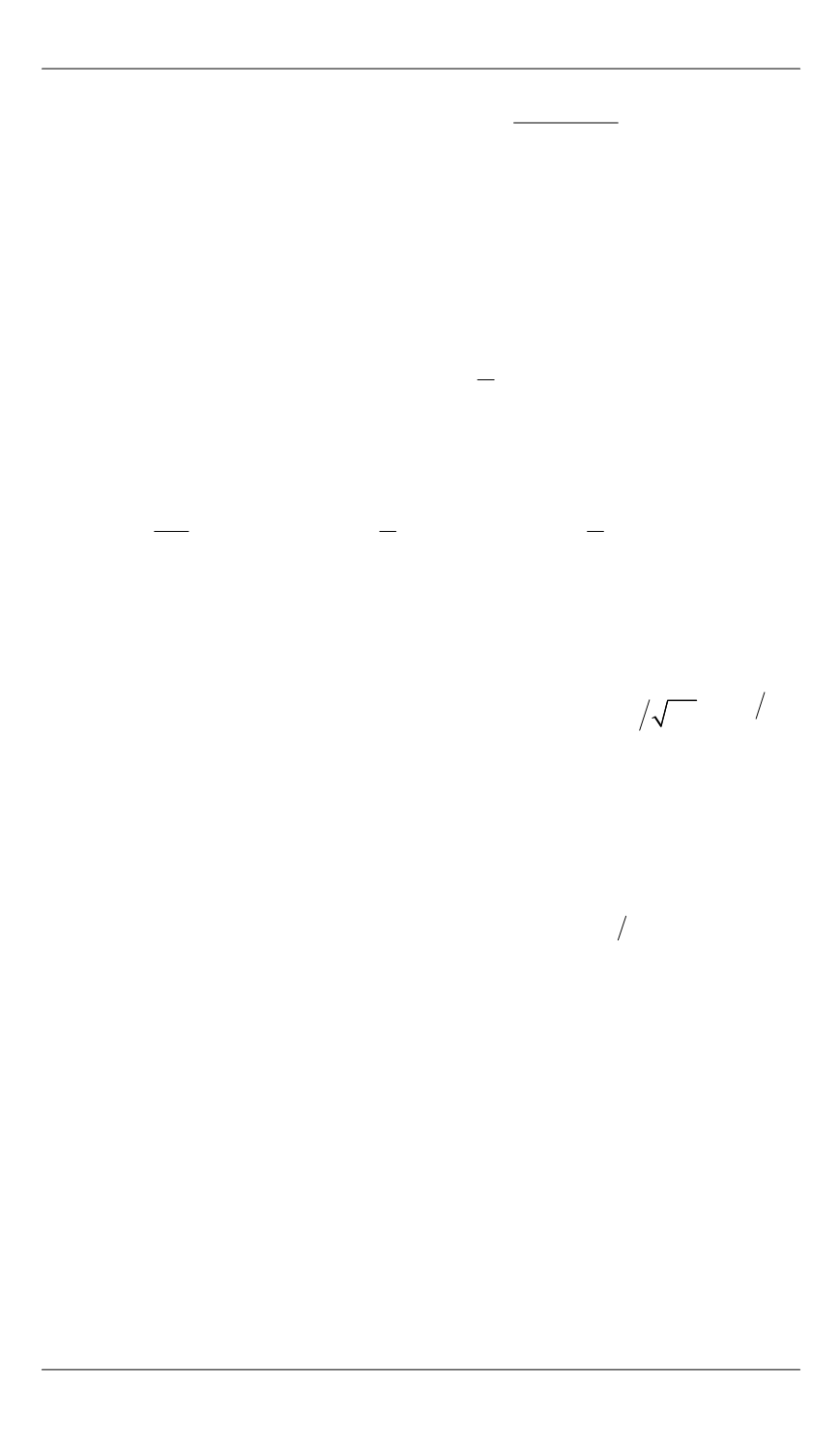
Алгоритм исследования нелинейных систем автоматического управления…
9
1
1
0;
2;
V
M V
2
2
2
1 .
1
f V
V
Согласно неканоническому разложению случайных функций, за-
кон распределения случайной величины
1
V
выберем нормальным.
Для случайной величины
2
V
с плотностью распределения вероятно-
стей
2
f V
используем известное
-преобразование к равномерному
закону [4]:
2
2
2
tg .
2
V V
V
В результате неканонического представления случайной функции
( )
Y t
исходное дифференциальное уравнение примет вид
2
1
2
2 sin tg
cos tg
,
2
2
dX bX
V t V
V t
dt
где
1
V
имеет стандартную форму нормального закона распределения,
а
2
V
— равномерного закона распределения.
Ортонормированная система многочленов с весовой функцией,
равной плотности случайной величины
1
V
2
1
2
1
1 2
,
V
f V
e
представляет собой полиномы Эрмита:
1
1 0
1;
V
P V
1
1
1
1
;
V
P V V
1
2
1
1
2
0, 707 0, 707;
V
P V
V
1
3
1
1
1
3
0, 408 1, 225 ;
V
P V
V
V
1
4
2
1
1
1
4
0, 204 1, 225 0, 612.
V
P V
V
V
Ортонормированная система многочленов с весовой функцией,
равной плотности случайной величины
2
V
2
1 2 ,
f V
представля-
ет собой полиномы Лежандра
1, 1
:
2
2 0
1;
V
P V
2
2
2
1
1, 7321 ;
V
P V
V
2
2
2
2
2
3, 3541 1,118;
V
P V
V
2
3
1
2
2
3
6, 6144 3, 9686 ;
V
P V
V
V
2
4
2
1
2
2
4
13,125 11, 25 1,125.
V
P V
V
V
Следует отметить, что для каждой весовой функции, являющейся
плотностью распределения вероятности случайной величины, суще-
ствует единственная ортогональная (ортонормированная) система
многочленов [5].
Возьмем для
1
V
две выборки
1
2 ,
q
а для случайной величины
2
V
— пять
2
5 ,
q
т. е.
1 2
10.
N q q
Тогда выборки случайных
величин (корни соответствующих многочленов) и коэффициенты ин-
тегрирования (10) принимают следующие значения: