Ю.В. Журавлев
8
с вершиной
А
(
ra
,
ra
) и точками
О
(0, 0) и
В
(2
ra
, 0) на оси абсцисс.
Второму уравнению системы (13) соответствует гипербола с ветвями
2
и
3
и асимптотами
4
и
5
(см. рис. 2); асимптота
5
совпадает с осью
абсцисс; асимптота
4
наклонная с отрицательным угловым коэф-
фициентом –2
L
; центр гиперболы в точке
C
(
r
(
a
–
), 0).
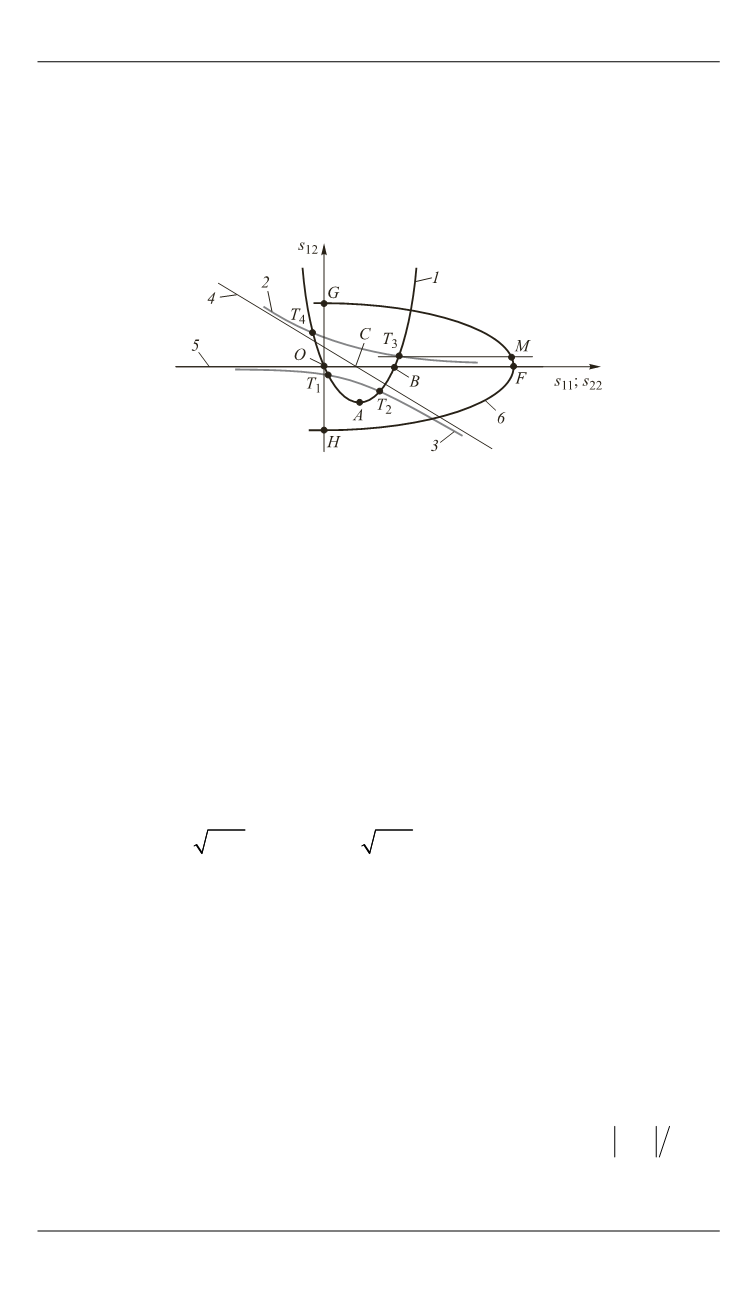
Рис. 2.
Графическое отображение системы (13)
Парабола
1
может пересекаться с ветвями гиперболы
2
и
3
макси-
мум в четырех точках
T
1,2,3,4
. Абсцисса точки
T
4
отрицательна, что не
отвечает решению системы (13), так как дисперсия
s
11
неотрицательна.
При достаточно большом значении
L
асимптота
4
будет иметь боль-
шую отрицательную крутизну –2
L
и пересечет ось абсцисс в точке
С
левее
О
, тогда точек
T
1,2
вовсе не будет. Из соображений непрерывно-
сти лишь точка
T
3
будет соответствовать искомому единственному
стационарному решению уравнений системы (13) с постоянными
a
и
b
. Координаты точки
T
3
дают искомые значения
s
11
и
s
12
.
Искомое значение
s
22
можно найти с помощью третьего уравне-
ния системы (13). На рис. 2 парабола, соответствующая этому урав-
нению, изображена кривой
6
с вершиной
F
(
2
, 0) на оси абсцисс
s
22
и
точками
G
(0,
2
r
) и
H
(0, – 2
r
) пересечения c осью ординат.
Точку
T
3
спроецируем параллельно оси абсцисс на кривую
6
и полу-
чим точку
M
(
s
22
,
s
12
) c абсциссой, равной искомому значению
s
22
дис-
персии погрешности оценки второй координаты состояния.
Отметим, что с ростом
L
ветви
2
и
3
гиперболы все плотнее
прижимаются к асимптотам
4
и
5
, причем асимптота
4
перемещает-
ся влево с одновременным разворотом по часовой стрелке, стремясь
занять параллельное оси ординат положение, а центр гиперболы
(точка
С
) может перейти на отрицательную часть оси абсцисс, при
этом
T
3
B
и
M
F
, т. е.
s
11
(–4
r L
/
L
),
s
22
σ
2
,
s
12
0.
Случай 2 (медленный перехват).
Изучим случай достаточной
малости коэффициентов
a
(
t
),
b
(
t
), когда мала величина
( ) ( ) .
L t L t
Отбросив в системе (11) члены с
a
(
t
) и
b
(
t
), придем к упрощенной си-
стеме дифференциальных уравнений Риккати:


