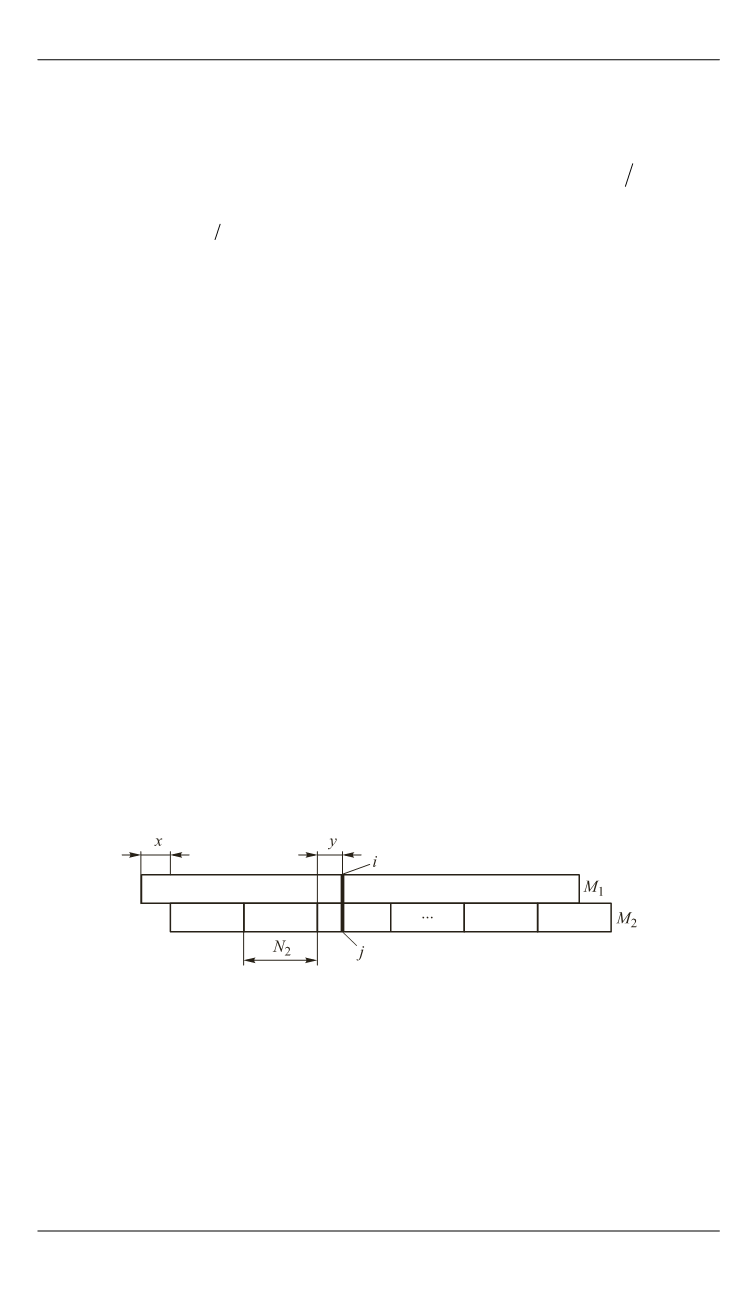
А.С. Косолапов, А.В. Второв
10
Система уравнений (12) связывает символы последовательно-
сти Касами с координатами
i
-го и
j
-го символов образующих ее
М-
последовательностей.
Поскольку число уравнений в системе (12), равное
3 2 ,
n
соот-
ветствует суммарному количеству всех координат элементов полей
2
n
GF
и
2
2
n
GF
, то она может быть решена относительно вели-
чин
i
b
и
j
b
. Таким образом, последовательность малого семейства
Касами разлагается на компоненты —
М-
последовательности. Затем
определяются номера текущих символов компонентных
М-
после-
довательностей с учетом изложенной методики. В итоге находятся
фаза и номер последовательности Касами, поступающей на вход
двухканального устройства обработки. Считая, что при формирова-
нии последовательности Касами одна из
М-
последовательностей (
М
1
)
длиной
1
N
является опорной, т. е. относительно нее сдвигается дру-
гая
М-
последовательность (
М
2
) длиной
2
N
, можно определить фазу
принятой последовательности Касами. Значение фазы соответствует
i
-му номеру символа опорной последовательности, рассчитанному в
одном из каналов обработки.
Обозначив через
j
номер символа второй
М-
последовательности,
рассчитанный в другом канале обработки в тот же момент времени,
можно записать
2
2
,
mod
mod
x i j
N
N
где
x
— сдвиг между компонентными
М-
последовательностями (
М
1
и
М
2
), т. е. номер опознанной последовательности Касами.
Нахождение величины
x
поясняется на рис. 7.
Рис. 7.
Определение номера последовательности малого семейства Касами
Величина
x
определяется выражением
2
,
mod
x
N
i y
где
2
.
mod
y j
N
Таким образом решается задача синхронизации и распознавания
составной кодовой последовательности.