А.А. Пожалостин, Б.Г. Кулешов, А.В. Паншина
6
эквивалентной системы
0 2
экв
1
1
2
i i
i
y
и
i
-е слагаемое в разложе-
нии функции Рэлея для продольных колебаний балки
2
2
0
1
.
2
l
i
i i
i
f dx s
Получим
0
.
i
i
i
f
Дифференциальное уравнение вынужденных поперечных коле-
баний для эквивалентной системы примет вид
0
0
0
,
i
i
i
i
i
i
i
m y
y c y Q
(7)
где
0
0
( (
) ( )
cos(
) ( ).
l
k k
i
i
i
i
i
F r
Q
F x x f x dx F pt
f x
y
(8)
Уравнение (7) с учетом выражения (8) принимает вид
2
2
cos(
),
i
i i
i i
i
y n y
y h pt
(9)
где
0 0
2
/
,
i
i
i
n
m
2 0 0
/
i
i
i
c m
— собственные частоты продольных
колебаний без трения.
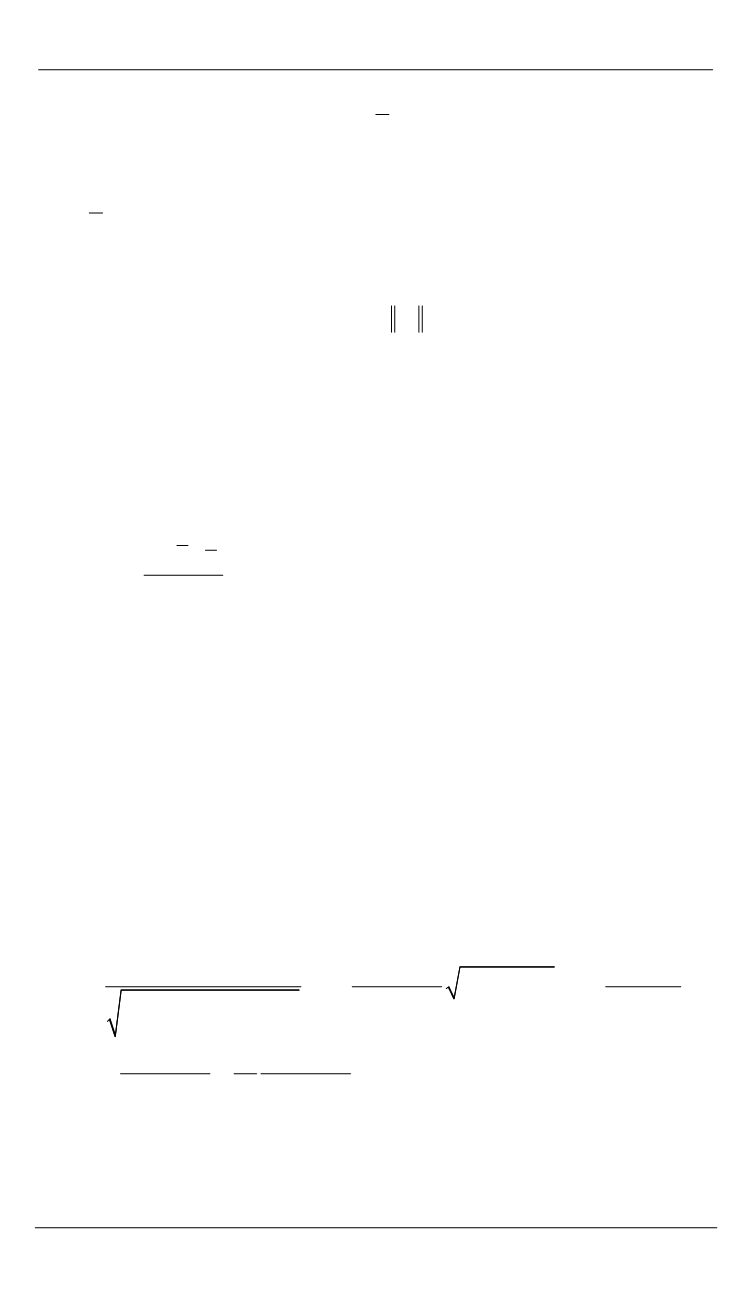
Частное решение уравнения (9) представим следующим образом:
cos(
),
i
i
i
y B pt
где
i
B
— амплитуда вынужденных колебаний:
0
2 2 2
0
2 2
2
2 2
2 2
2 2
2 2
1
( )
,
,
4
2
tg
.
i
i i
i
i
i
i
i
i
i
i
i
i
i
i
i
i
h
F f x
B
h
p h
m
p
p
n p
n p
p
A p
p
Здесь
i
— некоторые константы.
Рассмотрим теперь уравнение переходного процесса. Общее ре-
шение неоднородного уравнения имеет вид


