В.В. Андронов
2
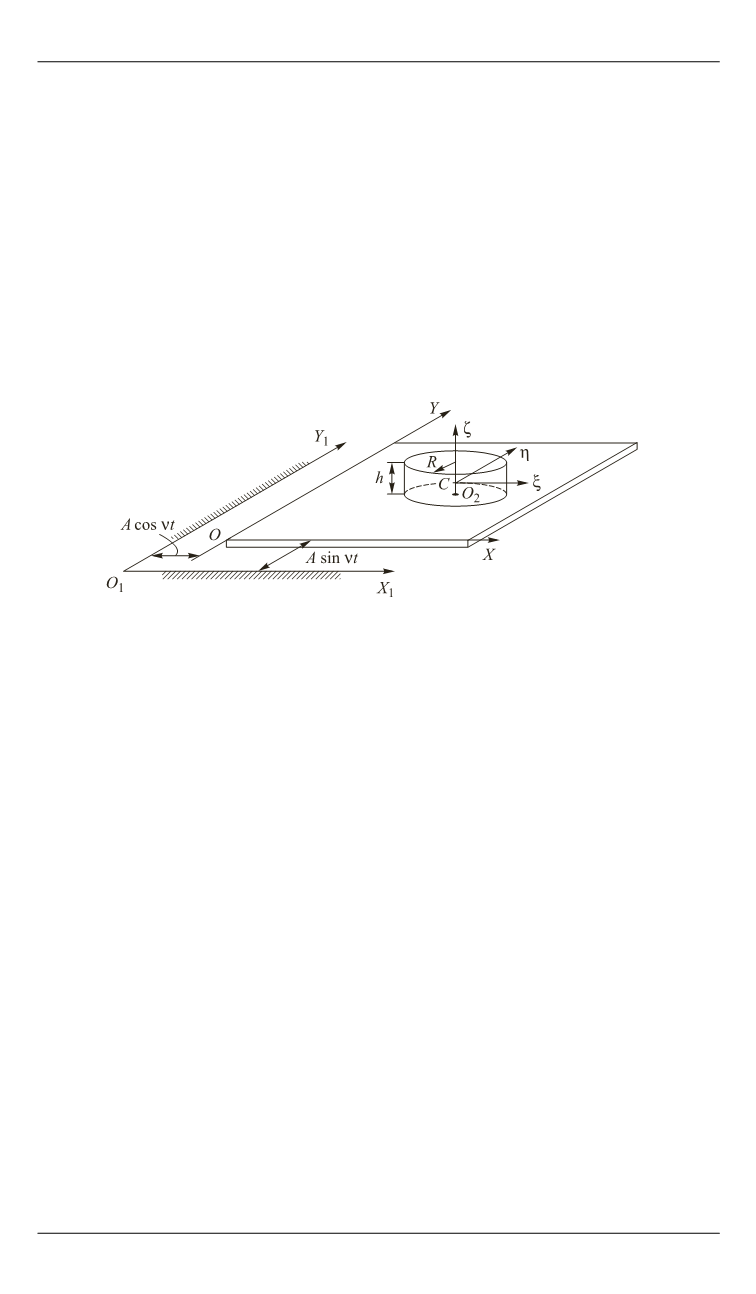
неизменно связанные с подвижной плоскостью и соответственно па-
раллельные осям неподвижной системы;
С
ξης
— система осей Кени-
га (рис. 1). При круговых колебаниях все точки подвижной плоскости
движутся по окружностям одинакового радиуса
A
с частотой
ν
со-
гласно уравнениям
1
10
1 10
сos ,
sin ,
X X A t Y Y A t
= + ν = + ν
(1)
где
1 1 10 10
, ,
,
X Y X Y
— координаты какой-либо точки вибрирующей
плоскости и центра ее круговой траектории в неподвижной системе
координат. Уравнения (1) одновременно являются уравнениями дви-
жения самой колеблющейся плоскости.
Рис. 1.
Цилиндрическое тело на вибрирующей шероховатой опоре
(
О
2
— центр основания цилиндра)
При колебаниях невысокой интенсивности первоначально непо-
движное относительно плоскости тело продолжает оставаться в от-
носительном покое. Если интенсивность колебаний достаточно вы-
сока, относительный покой невозможен, и тело будет скользить по
плоскости. Дифференциальные уравнения этого относительного
движения имеют вид
2
2
cos
,
sin
,
,
C
X
C
Y
z
z
mX mA t T
mY mA t T
J M
= ν ν +
= ν ν +
ϕ =
(2)
где
m
— масса тела (цилиндра);
,
C C
X Y
— координаты центра масс
тела в осях
;
OXYZ
,
X Y
T T
— проекции на эти оси силы трения (глав-
ного вектора сил трения, распределенных по площадке контакта тела
с опорной плоскостью);
z
J
— момент инерции тела относительно
оси симметрии;
z
М
— момент трения (алгебраический главный мо-
мент этих сил относительно центра основания цилиндра); первые
слагаемые в правых частях двух первых уравнений определяют соот-
ветствующие проекции переносной силы инерции.


