И.А. Мочалов, М.С. Хрисат
4
откуда
[ ]
(
)
H
1
1
( )
( ); ( )
( ) /
0;1
a a r y r a r y r r
= =
=
∈
,
поэтому
( )
( ) ( )
( )
[ ]
(
)
2
2
1H 1
2
1
1
2
1
0, 5
;
0,5
/
0;1
x x r
x y r x r
x y r r
=
= +
= +
∈
.
Аналогично находим
b
и далее
x
1Н
:
( )
( ) ( )
( )
[ ]
(
)
2
1H 1
2
2
1
2
2
0, 5
;
0, 5
/
0;1 .
x x r
x y r x r
x y r r
=
= +
= +
∈
Это означает, что фазовые траектории являются нечеткими пара-
болами.
Находим нечеткое время
T
Н
=
τ
1Н
+
τ
2Н
, затрачиваемое на переход
из нечеткой точки. Здесь
τ
1Н
,
τ
2Н
— нечеткие времена движения соот-
ветственно при
*
H H
1
u
=
и
*
H
H
1
u
= −
(рис. 2).
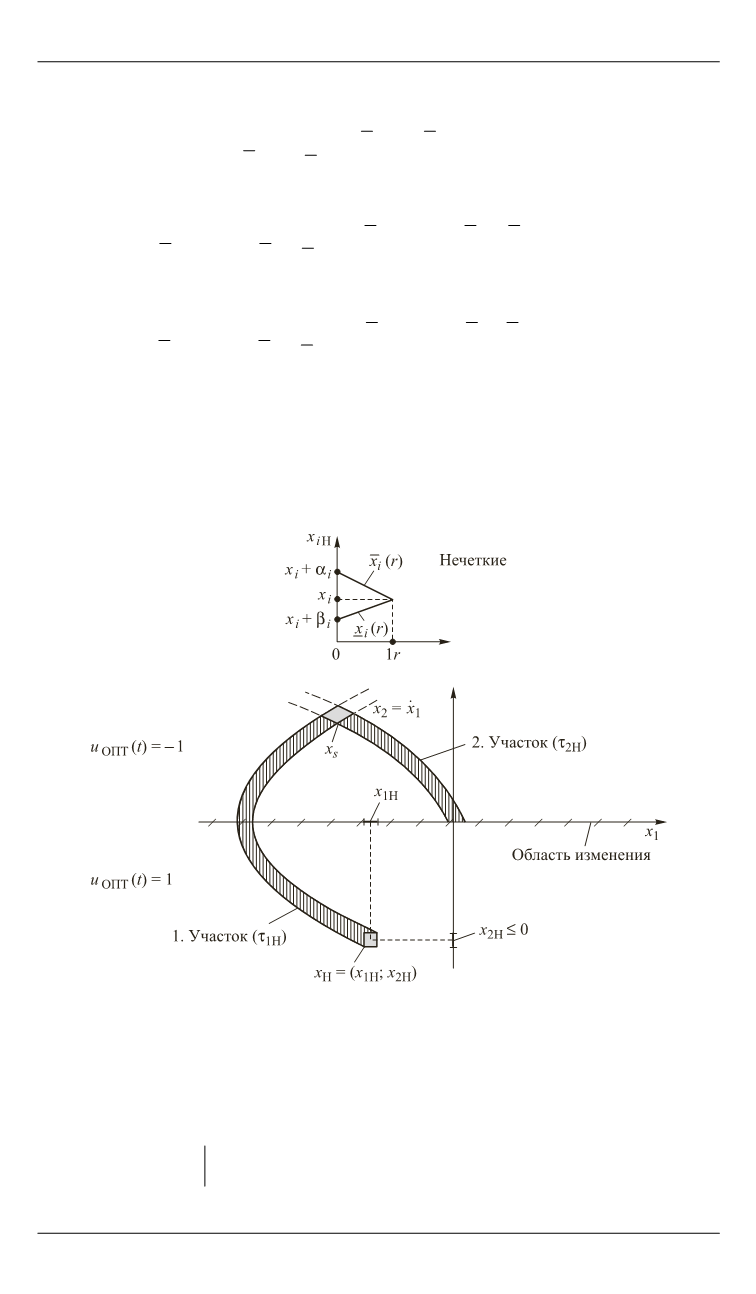
Рис. 2.
Оптимальная нечеткая траектория в задаче о быстродействии
На первом участке перехода
x
Н
→
x
s
при
*
H H
1
u
=
имеем
*
H
1
2
2
2
1
1
1
2
2
1
( )
( ) 0,5
.
u u
x x
x t t c x t
t
c t c
x u
= =
=⎧⎪
→ = + → = + +
⎨
= ⎪⎩


