И.А. Мочалов, М.С. Хрисат
2
где
( )
(
)
( )
2
1
1
, ,
,
t
t
I
L x u t dt L
⋅ =
⋅
∫
— интегрант,
I
2
(·) — терминальный
член. Необходимо найти min
u
(
t
)
I
(
x
,
u
,
t
) или, в символической форме,
М = НГУ =
I
→ min
I
, где M — модель; НГУ — нечеткие граничные
условия;
I
— функционал. Для получения интерпретируемых в гео-
метрической форме результатов рассмотрим частную задачу об успо-
коении материальной точки [6,7], для которой решается нечеткая за-
дача о быстродействии (нечеткая задача Лагранжа).
Имеем
1)
1
2
2
x x
x u
=⎧
⎨
= ⎩
— модель объекта управления;
u
— управление;
2)
(
)
( ) ( )
[ ]
(
)
(
)
( ) ( )
[ ]
(
)
1
1Н 1
1
2
2H 2
2
0
,
/
0;1 ;
0
,
/
0;1
x t
x x r x r r
x t
x
x r x r r
= = =
∈
= = =
∈
—
нечеткие граничные условия, представленные в уровневой фор-
ме, H — индекс нечеткости;
3)
1
u
≤
— ограничение на управление;
4)
H
H
0
T
I
dt T
= =
∫
— функционал качества управления.
В условиях (1– 4) необходимо найти min
u
T
H
(рис. 1).
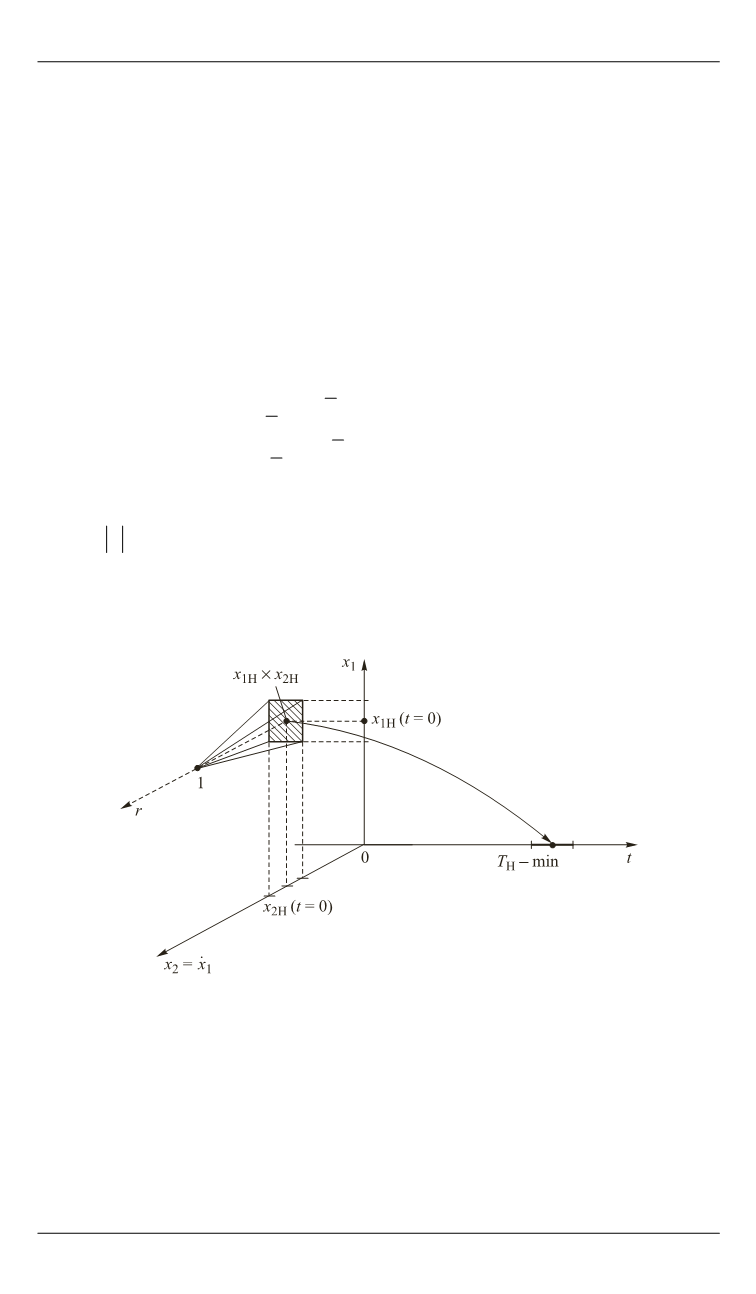
Рис. 1.
Задача о быстродействии (задача Лагранжа):
0
min
H
T
H
I dt T
= −
∫
при нечетких граничных условиях
x
1H
,
x
2H
2. Метод решения.
В соответствии с принципом максимума име-
ем функцию Гамильтона
1 2
2
( )
1
H u
x
u
= Ψ + Ψ −
,


