Скользящие теоретико-числовые преобразования Рейдера
7
ских БТЧП. На нем используется нечетная промежуточная выбор-
ка
1
1
1
(
) ( 2 1)
x j i
x j
i
− = − −
. Ее можно записать так:
1
[( 1) 2 ]
x j
i
− −
, и
тогда она совпадет с четной выборкой на предыдущем (
j
–1)-м шаге
скольжения,
т. е.
будет
справедливо
равенство
1
1
(
)
x j i
− =
0
1
[( 1) ]
x j
i
− −
. Но в этом случае ее спектр
(1)
1
( )
j
X k
(см. си-
стему уравнений (3)) будет равен
[
]
(
)
(
)
1 1
1
/2 1
(1)
(0)
2
/2
1
0
1
1 1
0
( )
( 1)
2
( ) mod 2 1
N
i k
N
j
j
i
X k
x i
i
X k
−
−
=
≡
− −
≡
+
∑
.
. .
. .
. . .
. . .
. . .
. . .
. .
. .
x
(
j
)
x
(
j–
4)
x
(
j–
2)
x
(
j–
6)
x
(
j–
1)
x
(
j–
5)
. . . .
. . .
. . . .
.
x
(
j–
3)
x
(
j–
7)
Х
j
(0)
Х
j
(1)
Х
j
(2)
Х
j
(3)
Х
j
(4)
Х
j
(5)
Х
j
(6)
Х
j
(7)
4
4
4
2
8
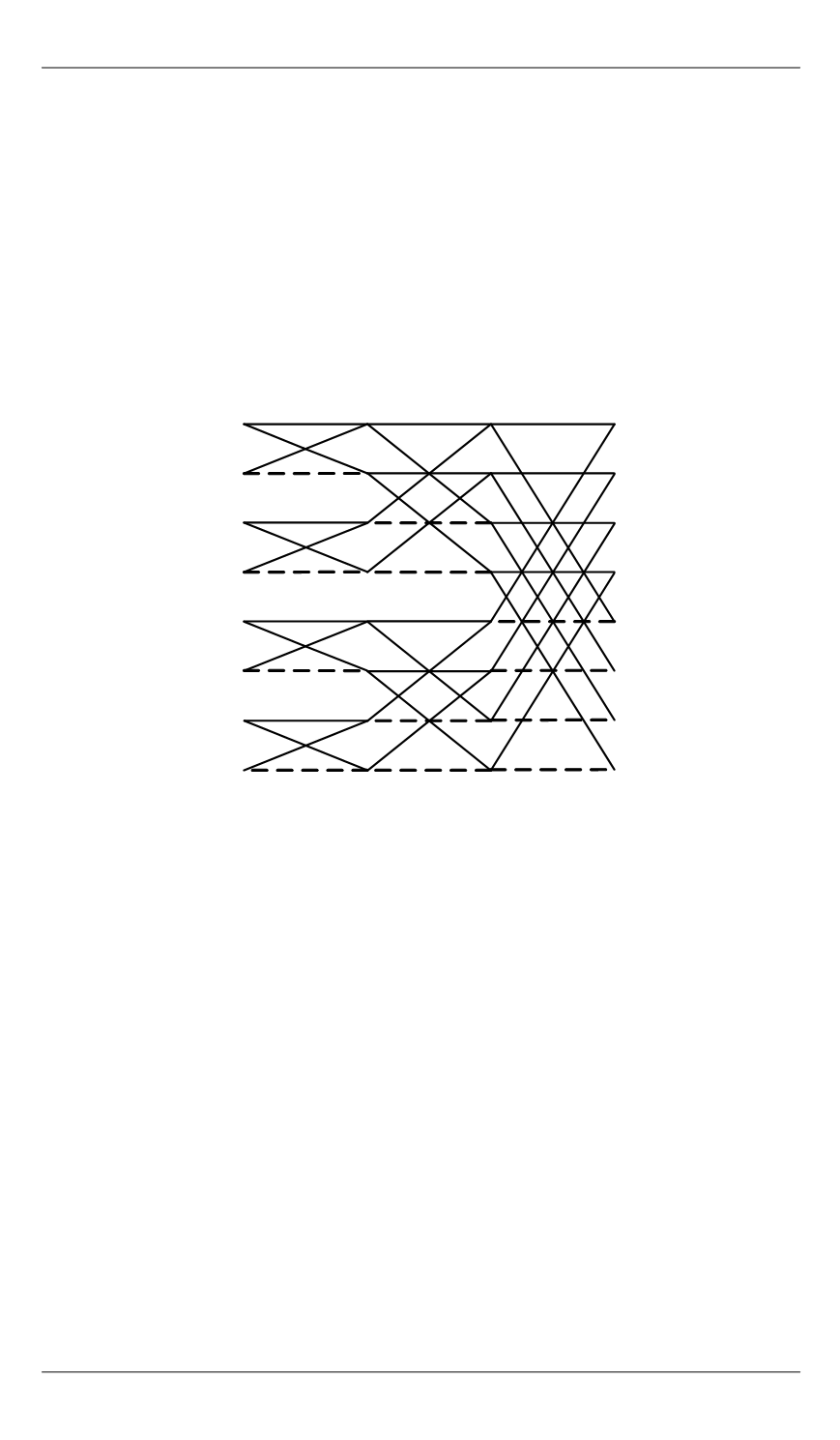
Рис. 1.
Сигнальный граф полного статического алгоритма БТЧП Рейдера
для
8
N
=
Тогда и алгоритм (2) БТЧП на этом уровне прореживания примет
следующий вид:
(
)
(
)
(
)
(
)
1
1
(0)
(0)
/2
1
1
1 1
(0)
(0)
/2
1
1
1 1
( )
( ) 2
( ) mod 2 1 ,
(
/ 2)
( ) 2
( ) mod 2 1 .
k
N
j
j
j
k
N
j
j
j
X k X k
X k
X k N X k
X k
−
−
≡
+
+
+
≡
−
+
(8)
Если в нем промежуточный спектр
(0)
1 1
( )
j
X k
−
, полученный на преды-
дущем шаге скольжения, сохранить, то при реализации алгоритма (8)
нужно будет вычислять только промежуточный спектр четной теку-
щей промежуточной выборки. Это позволит почти в 2 раза умень-
шить число вычислительных операций.
Очевидно, такой подход можно использовать и на других уров-
нях прореживания, получая дополнительную экономию вычислений.
В общем случае на
m
-м уровне прореживания промежуточные вы-
борки равны (см. соотношения (6)):


