В.В. Сюзев
10
. .
. .
. . . . . . . . . .
. . . .
. . . .
X
j
(0)
X
j
(3)
X
j
(1)
X
j
(2)
X
j
(5)
X
j
(4)
X
j
(7)
X
j
(6)
x
(
j
)
x
(
j–
4)
2
4
8
4
(2)
2
(0)
j
X
−
(2)
2
(1)
j
X
−
(1)
1
(0)
j
X
−
(1)
1
(1)
j
X
−
(1)
1
(2)
j
X
−
(1)
1
(3)
j
X
−
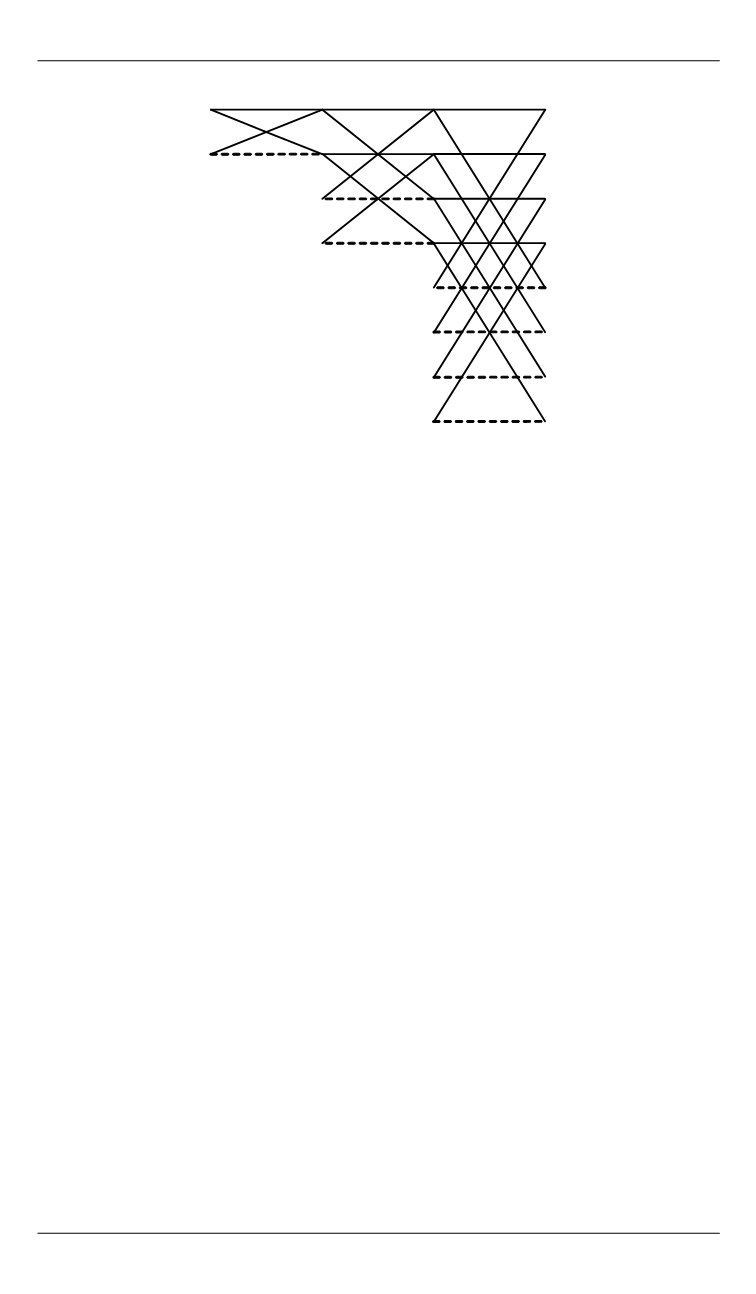
Рис. 2.
Сигнальный граф полного скользящего алгоритма БТЧП Рейдера
для
8
N
=
Заключение.
Поставлена теоретико-прикладная задача синтеза
алгоритмов быстрого анализа теоретико-числового спектра Рейдера
на скользящих интервалах времени. В рамках ее решения получены
следующие научные и практические результаты. На основе скалярно-
го представления теоретико-числовых преобразований приведено
общее аналитическое описание статических быстрых преобразований
Рейдера (БПР) для скользящих выборок на произвольных уровнях
прореживания. Путем их модификации с учетом результатов анализа
спектра на предыдущих шагах скольжения разработаны общие ори-
гинальные алгоритмы скользящих БПР. Получены аналитические
оценки вычислительной сложности этих алгоритмов и показана их
высокая эффективность при больших объемах выборок обрабатывае-
мых сигналов. Проиллюстрирована целесообразность наглядного
графического представления скользящих БПР в виде специальных
сигнальных графов, разработана их структура. Полученные теорети-
ческие результаты подтверждены конкретными примерами.
Разработанный в статье класс быстрых преобразований Рейдера
ориентирован на обработку высокочастотных сигналов больших объ-
емов по методу «скользящего окна» в вычислительных системах ре-
ального времени.
ЛИТЕРАТУРА
[1] Оппенгейм А., Шафер Р.
Цифровая обработка сигналов
. Москва, Техно-
сфера, 2007, 856 с.
[2] Айфичер Э., Джервис Б.
Цифровая обработка сигналов: практический
подход
. 2-е изд. Москва, Издательский дом «Вильямс», 2004, 992 с.


