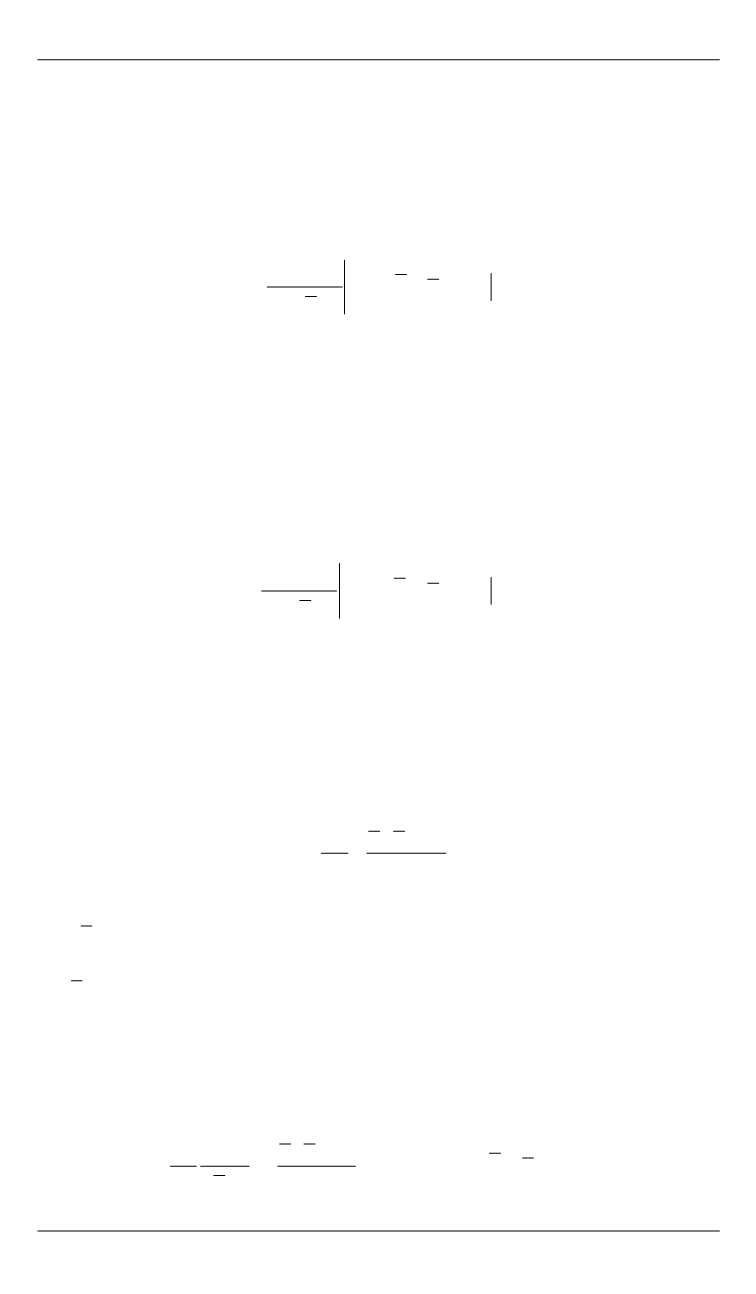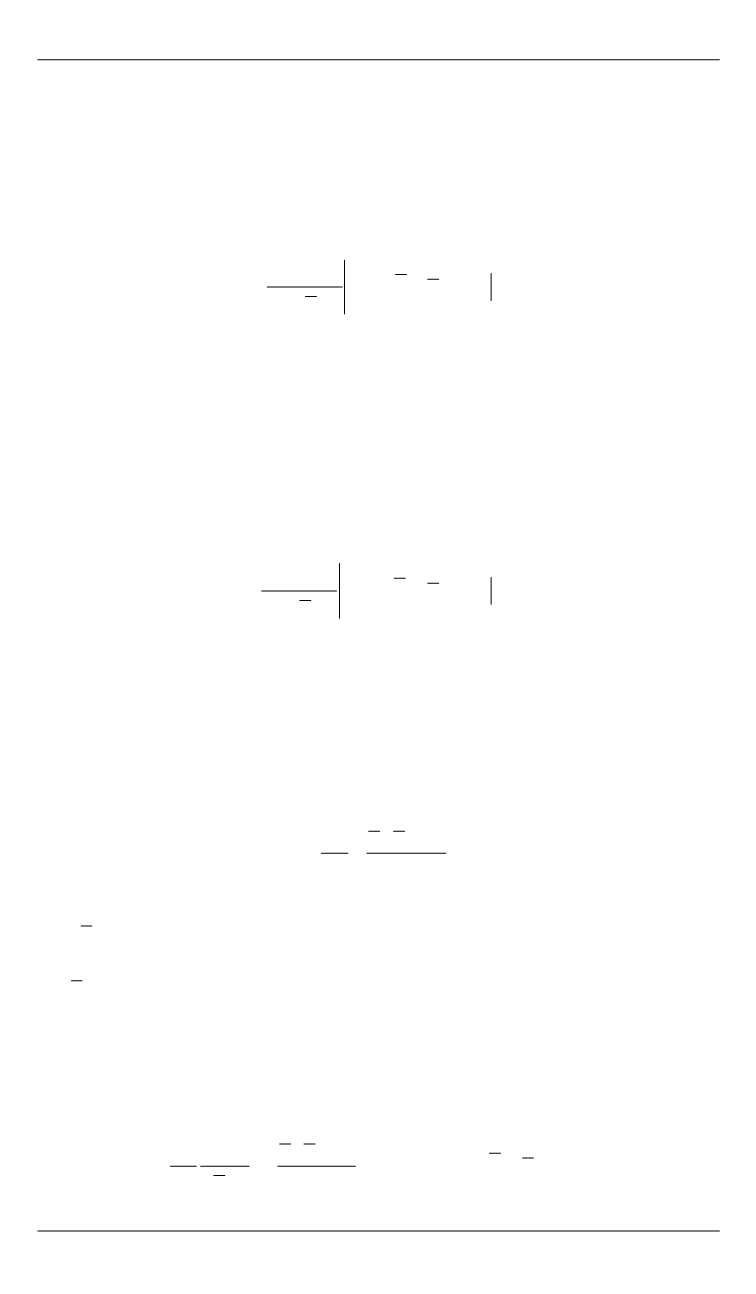
В.Н. Тимофеев, А.Ю. Бушуев
4
0,
где
– оператор Лапласа.
Подстановка выражения (3) в граничное условие непротекания
(2) приводит к следующему соотношению на поверхности эквива-
лентного тела:
0
0
( )
( ) .
M V n M
n
(4)
Учитывая граничные условия непротекания поверхности эквива-
лентного тела ,
записанные в форме (4), и граничные условия зату-
хания возмущений на бесконечности получаем, что потенциал воз-
мущенных скоростей
0
( )
M
является решением внешней задачи
Неймана для уравнения Лапласа:
0
Δ ( ) 0,
M
(5)
0
0
( )
( ) ,
M V n M
n
(6)
0
0
( ) 0,
,
M M
(7)
0
0
( ) 0,
.
M M
(8)
Внешняя задача Неймана имеет единственное решение, которое
найдем в виде потенциала двойного слоя
0
3
1
( )
( )
( ) ,
4
r n M
M
g M d
r
(9)
где
r
– вектор, направленный из точки
М
, расположенной на элемен-
те площади
d
, в точку вычисления скорости
M
0
;
r
– модуль векто-
ра
r
;
( )
g M
– поверхностная плотность потенциала двойного слоя.
Потенциал двойного слоя удовлетворяет уравнению Лапласа (5) и
граничным условиям (7)–(8) затухания возмущений на бесконечно-
сти. Граничное условие непротекания (6) выполняется, если поверх-
ностная плотность
( )
g M
удовлетворяет интегральному уравнению
0
0
3
1
( ) ( )
( ).
4
M
r n M g M d V n M
n
r