О резонансном режиме в нестационарной задаче о подвижной нагрузке …
5
Интеграл (13) может быть записан в терминах элементарных
функций:
0 1
1
1
2 2 2
1
1
1
1
1
(
)
(
)
(0)
, , ,
,
2 (
) 2 (
)
R
AP k z
g ik z
g ik z
g
y z t
c
ik z ik z ik z ik z
k z
(14)
где
2
1
2
2 2 2
2
1
2
2
2 2 2
2 2 2
tanh
.
R
R
R
s
R
R
R
R
R
R s
g s
s c t
c t
y s c t
r s c t
y sc t
c t
y s c t
c t
y r c t
Потенциалы
,
1, 2
m
m
могут быть восстановлены с ис-
пользованием соотношений (4). Затем, используя (5), можно найти
выражения для компонент перемещения. Рассмотрим подробно вер-
тикальное перемещение
z
u
. Из (4) и (5) получим
1
2
2
2
, , ,
, , ,
2
,
1
z
t x y k z
t x y k z
u
z
z
k
(15)
где функция
1
, , ,
t x y k z
определена в (14).
На графиках (рис. 2–4) проиллюстрированы полученные ре-
зультаты. При их построении были использованы следующие зна-
чения упругих параметров материала:
1
5970
c
м/с,
2
3763
c
м/с,
3409
R
с
м/с, что соответствует SiO
2
[16].
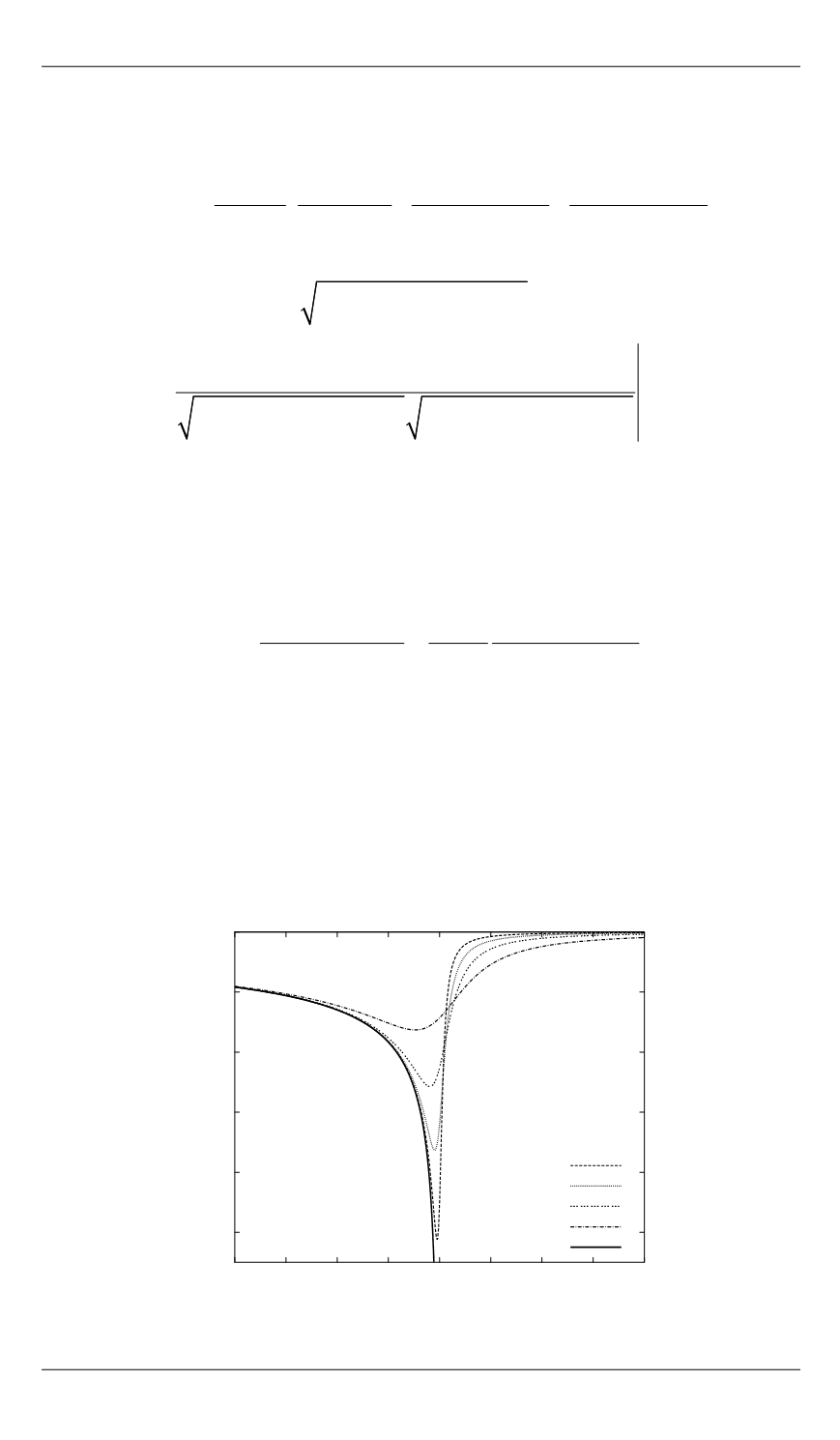
Рис. 2.
Зависимость потенциала
от подвижной координаты
( 1,
10)
y t
-1000
-800
-600
-400
-200
0
-20 -15 -10 -5 0 5 10 15 20
z = 0.5
z = 1
z = 2
z = 5
z = 0


