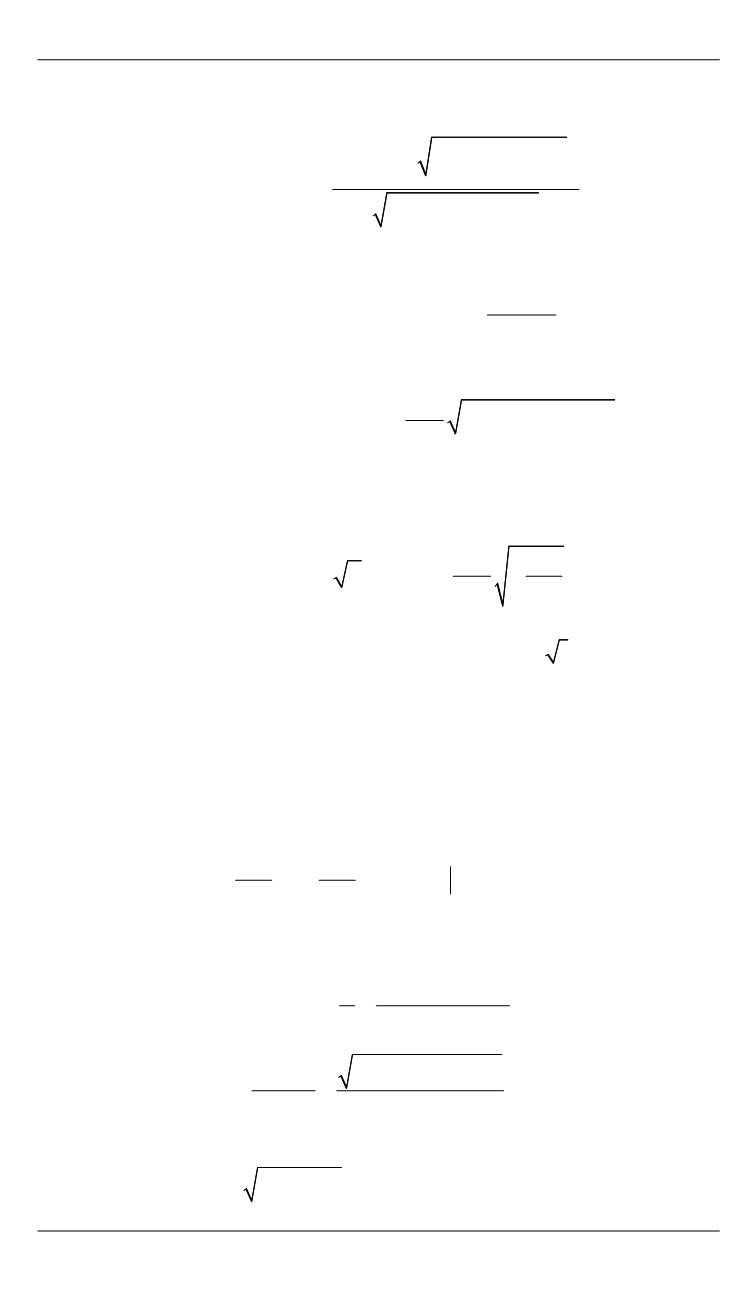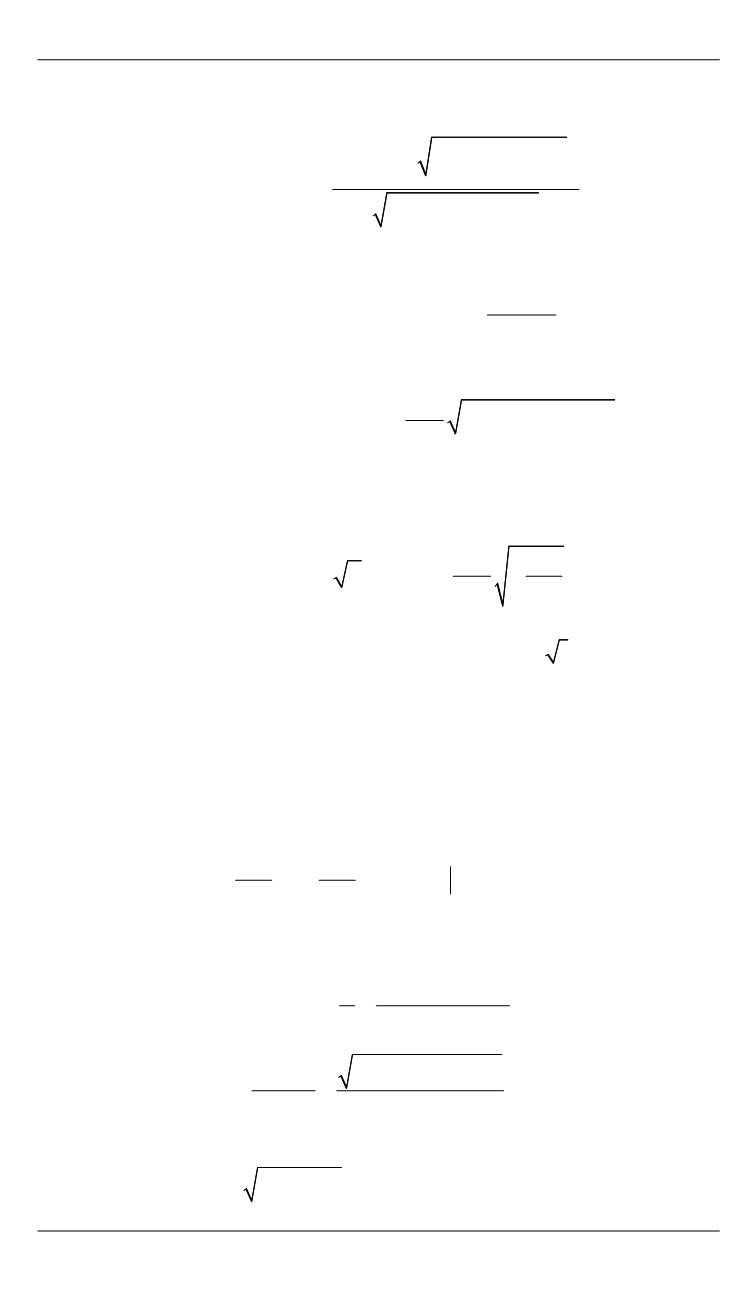
Т.В. Облакова, Д.А. Приказчиков
4
Переходя в подвижную систему координат
, ,
y
получим
2 2
0
2 2
0
, , 0,
,
2
t
R
R
R
H c s
c s y
y t
AP
ds
sc y
(9)
где
;
.
R
x c t s t
Интегрируя (9) при условии
2 2
0,
,
2
R
y
t
c
найдем значе-
ние потенциала
на поверхности
z
= 0:
2
2
0
0
, ,
, , 0,
2
.
R
R
AP
y t
y t
c t
y
c
(10)
Найденное решение представляет интерес в первую очередь для
исследования развития резонансных явлений во времени. При
t
0
0
2
, ,
,
,
R
R
AP c
y t
C t
C
c
(11)
т. е. значение потенциала растет по времени как
O t
, что отличает
полученное трехмерное решение от соответствующего решения
плоской задачи, характеризующейся линейным ростом.
Используя значение потенциала на поверхности
z
= 0, восстано-
вим его значение вглубь полупространства. По аналогии с [12] можно
рассматривать параметрическую зависимость от переменной
y
, и та-
ким образом, рассматривать задачу Дирихле вида
2
2
2
1
0 0
2
2
0,
.
z
k
z
(12)
Применяя формулу Пуассона, получим
2
1
2
1
1 0
2 2 2
1
2
2
0 1
2 2 2
1
, ,
1
, , ,
2
,
s
s
s
R
R s
k z r y t
y z t
dr
r
k z
r
c tr y
AP k z
dr
c r r
k z
(13)
где
2 2 2
1
, ( 1, 2)
m
m R
R
s
c t
c t
y m
.