О резонансном режиме в нестационарной задаче о подвижной нагрузке …
3
При этом поле перемещений выражается в терминах введенных
потенциалов [15] как
1
2
1
2
,
,
x
y
z
u
u
u
x z
y z
z
x
y
. (5)
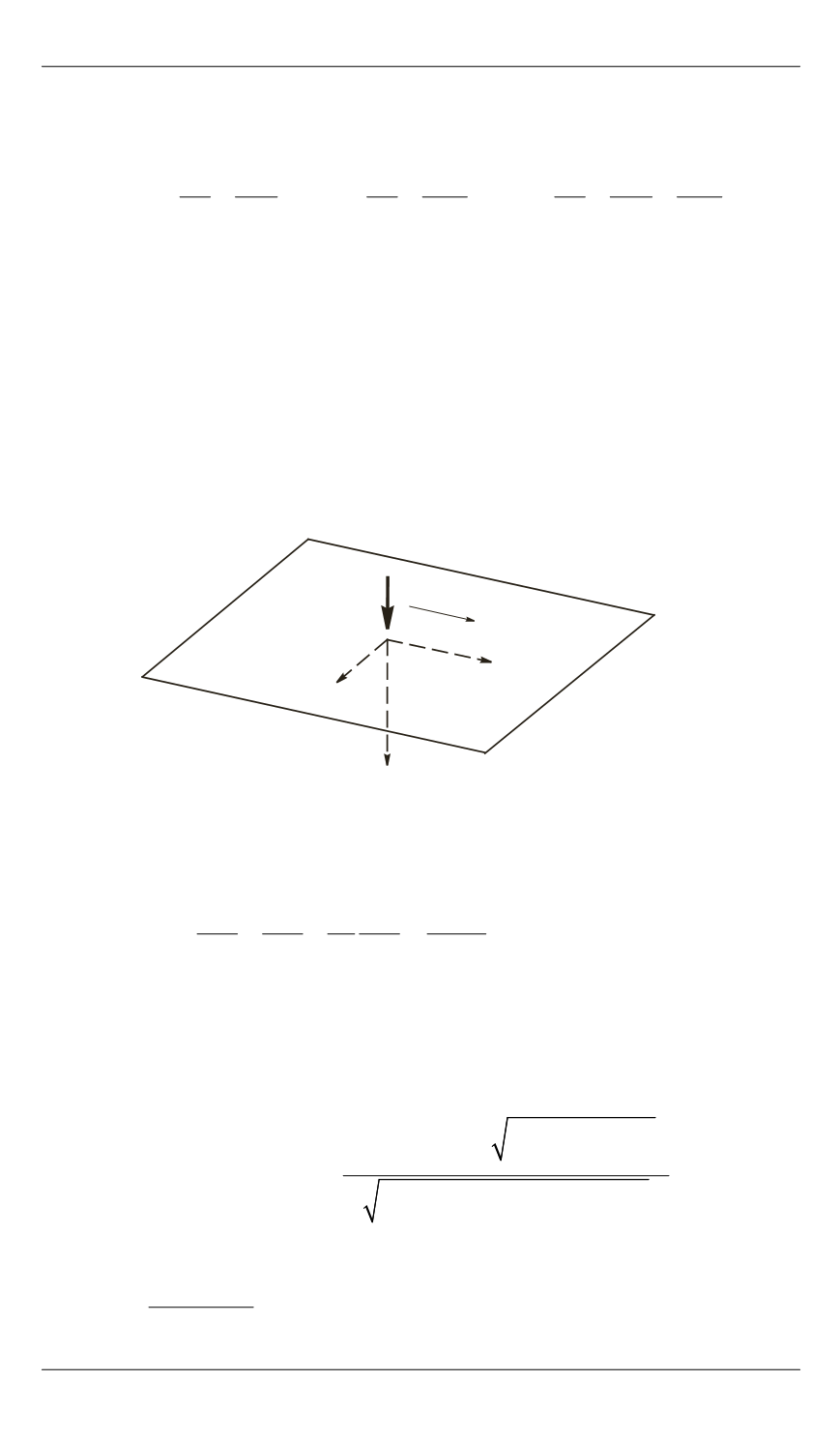
Нестационарная задача о подвижной нагрузке для упругого
полупространства.
Рассмотрим задачу о движении с постоянной
скоростью импульсной подвижной нагрузки по поверхности
z
= 0.
Ограничимся здесь исследованием резонансного случая, когда ско-
рость движения нагрузки совпадает со скоростью волны Рэлея. В слу-
чае движения вдоль оси
Ox
функция
( , , )
P x y t
имеет вид (рис. 1)
0
( , , )
(
) ( )
R
P x y t
P x c t
y
.
(6)
Рис. 1.
Схема постановки задачи
Следовательно, уравнение (3) принимает вид
2
2
2
2
2
0
2
2 2 2
1
1
(
) ( ).
2
R
R
k P x c t
y
B
x y c t
(7)
Решение уравнения (7) по аналогии с решением в [3] может быть
записано через свертку с соответствующим фундаментальным реше-
нием:
2 2
0
2
2
2
2
0
, , 0,
,
t
R
R
R
R
H c t
x c t
y
x y t
AP
d
c t
x c t
y
(8)
где
2
2
1
4
R
c
k
A
B
.
c
x
y
P
z
R
0


