В.Ф. Апельцин
,
А.И. Полетаев
4
rot
H
+
i
E
=
e
j
;
rot
E
–
i
H
=
m
j
.
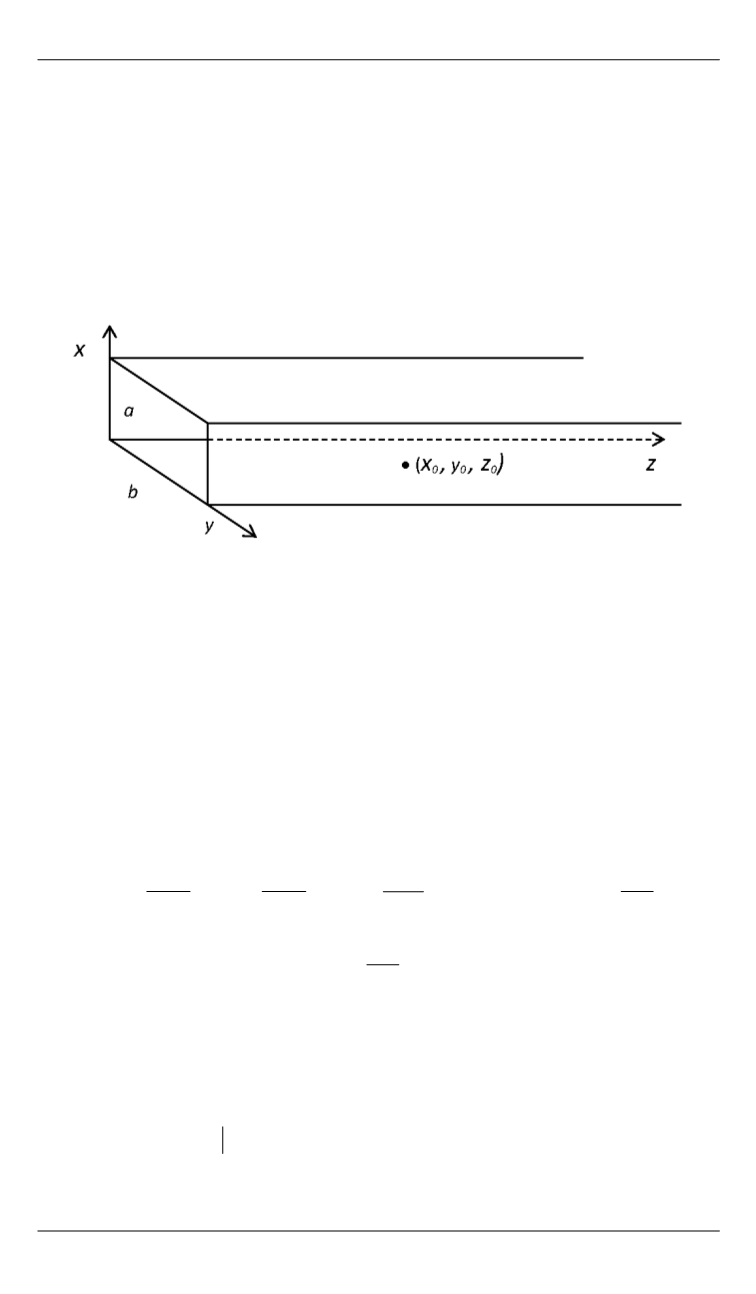
Бесконечный металлический прямоугольный волновод, внут-
ренность которого представляет собой неограниченную область
D
:{0
x
a
; 0
y
b
;
z
}, возбуждаемый полем точечного
источника, которым может являться электрический или магнитный
диполь (рисунок).
Геометрия задачи возбуждения прямоугольного волновода
дипольным точечным источником
1. Для случая электрического диполя
e
j
=
p
0
,
;
M M
m
j
= 0.
Задача допускает введение скалярного потенциала
( , , ),
U x y z
свя-
занного с векторным потенциалом
e
A
соотношением
e
A
=
i
×
×
( , , )
U x y z
.
z
e
Компоненты полей
Е
и
Н
вычисляются через
( , , )
U x y z
в стандартном виде:
x
E =
2
U
x z
;
y
E =
2
U
y z
;
z
E
=
2
2
U
z
+
2
k
;
U
x
H =
i
U
y
;
y
H
= i
U
x
;
z
H =
0.
Краевая задача для скалярного потенциала
( , , )
U x y z
(функции
Грина) имеет вид
2
0
0
0
;
0.
S
U k U x x y y z z
U
(3)
Здесь
S
– боковая поверхность волновода.


