Базовая сферическая линза с исправленной сферической аберрацией путем применения…
13
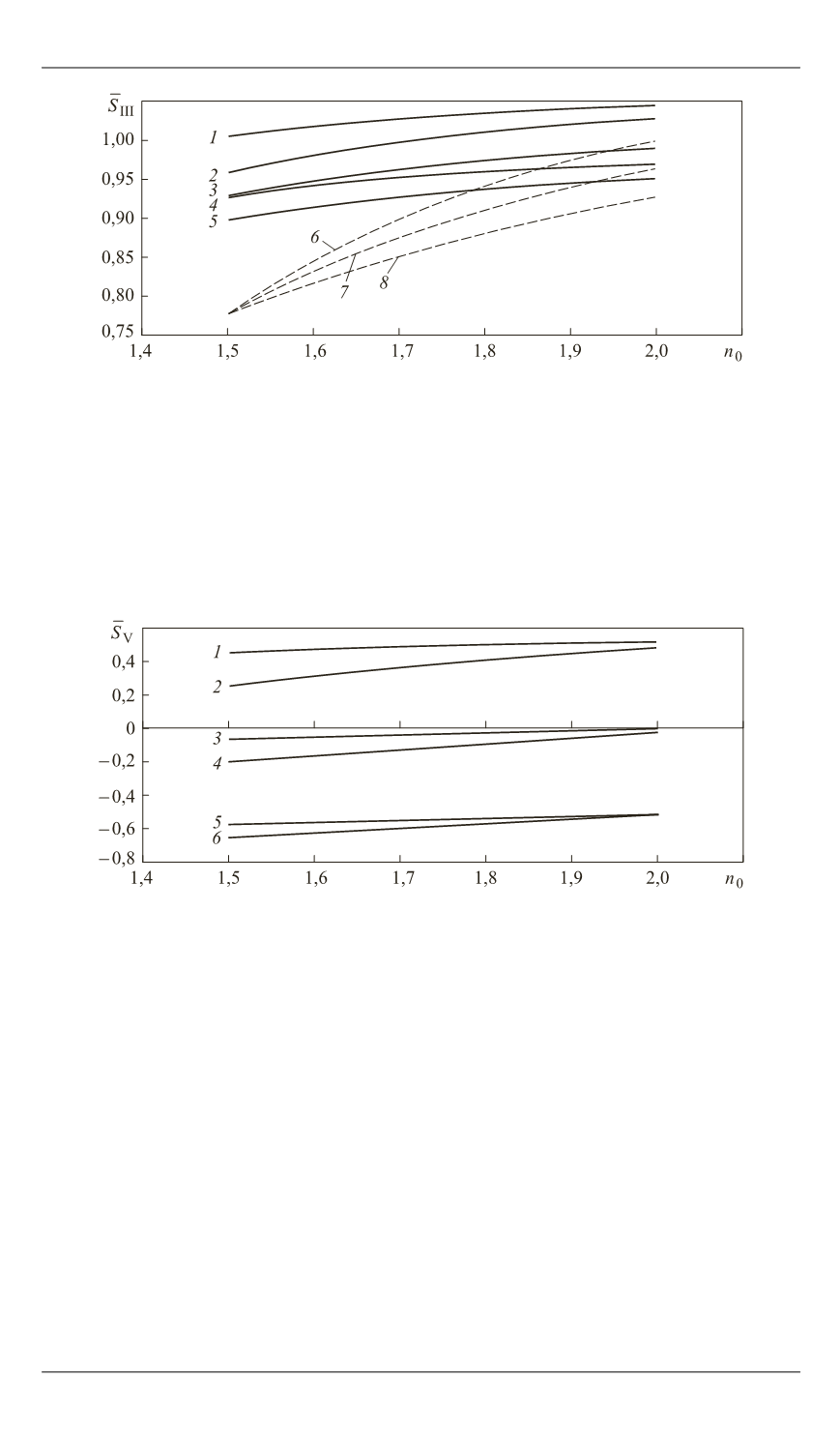
Рис. 4.
Изменение третьей суммы Зейделя линз семейств 1 и 2 в зависимо-
сти от
s
p
:
1
— однородная линза при
s
p
= 15 мм,
d
= 10 мм;
2
— градиентные линзы при
s
p
=
= 15 мм,
d
= 10 мм;
3
— однородная и градиентные линзы при
s
p
= 0 мм,
d
= 10 мм;
4
— однородная линза при
s
p
= –15 мм,
d
= 10 мм;
5
— градиентные линзы при
s
p
=
= –15 мм,
d
= 10 мм;
6
— градиентные линзы при
s
p
= 15 мм,
d
= 30 мм;
7
— одно-
родная и градиентные линзы при
s
p
= 0 мм,
d
= 30 мм;
8
— градиентные линзы при
s
p
= –15 мм,
d
= 30 мм
Рис. 5.
Изменение пятой суммы Зейделя линз семейств 1 и 2 в зависимости
от
s
p
:
1
— градиент на стрелке прогиба при
s
p
= 15 мм,
d
= 10 мм;
2
— градиент на стрел-
ке прогиба при
s
p
= 15 мм,
d
= 30 мм;
3 —
градиент на стрелке прогиба при
s
p
=
= 0 мм,
d
= 10 мм;
4
— градиент на стрелке прогиба при
s
p
= 0 мм,
d
= 30 мм;
5
—
градиент на стрелке прогиба при
s
p
= –15 мм,
d
= 10 мм;
6
— градиент на стрелке
прогиба при
s
p
= –15 мм,
d
= 30 мм
Другими словами, при
s
p
= 0 градиентные с ОЛРПП линзы с ис-
правленной сферической аберрацией в отношении комы, астигма-
тизма, кривизны и дисторсии третьего порядка сохраняют свойства
однородной линзы, рассчитанной на минимум сферической аберра-
ции третьего порядка. При этом все рассматриваемые линзы имеют
одинаковый радиус первой поверхности.
Вторая сумма градиентных линз не зависит от положения зрачка.
При изменении базового ПП
n
0
во всей области его допустимых зна-


