А.В. Плюснин
12
шения для тела простой формы (например, сфера), либо равны нулю,
поскольку слабо влияют (для режима сплошного обтекания ЛА) на
рассматриваемый процесс.
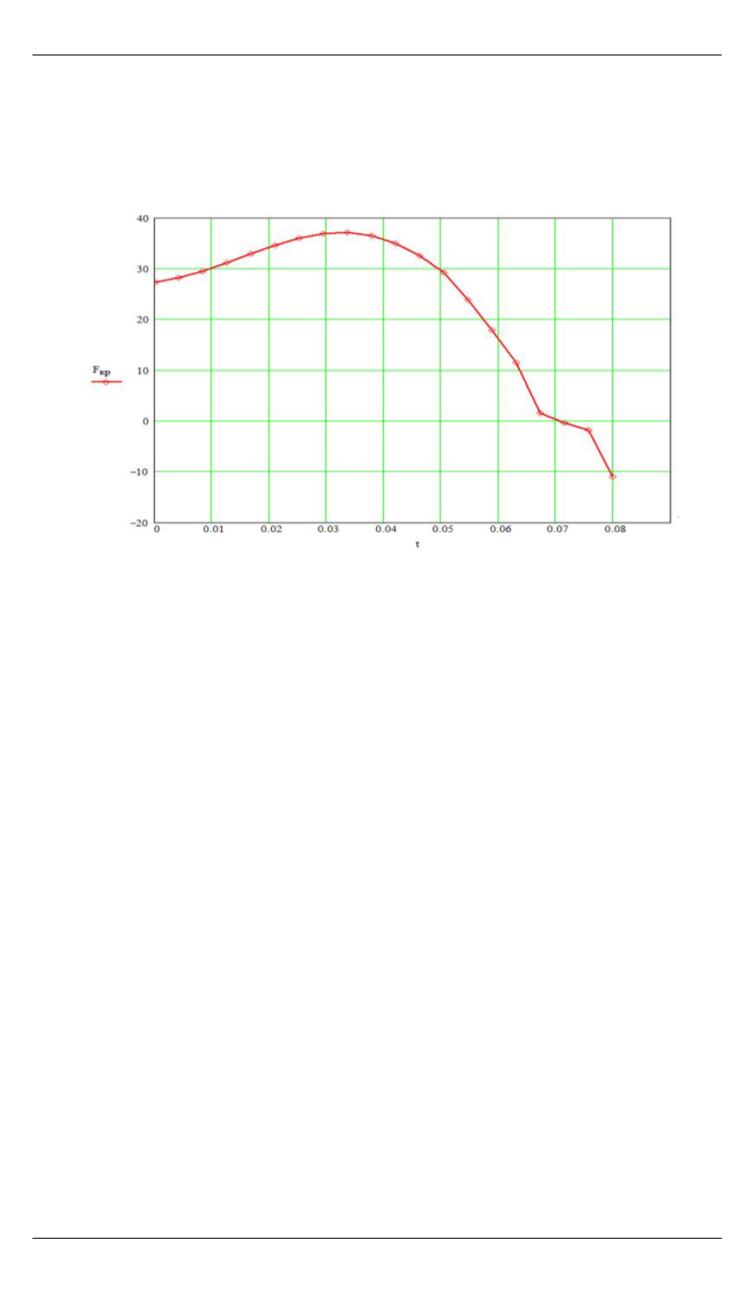
Результат расчета силы (по нормали к базовой плоскости крыш-
ки) показан на рис. 5.
Рис. 5.
Расчетное значение силы на крышку ПУ
Выводы.
В работе предложен метод расчета нестационарной
нагрузки на крышку пускового устройства при подводном выбросе
ЛА, основанный на методе граничных элементов. Он может быть ис-
пользован для более глубокого исследования рассматриваемого фи-
зического процесса на основе экспериментальных данных.
ЛИТЕРАТУРА
[1]
Апальков Ю.В., Мант Д.И., Мант С.Д.
Отечественные баллистические
ракеты морского базирования и их носители
. Санкт-Петербург, Галея
Принт, 2006, 216 с.
[2]
Дегтярь В.Г., Пегов В.И.
Гидродинамика подводного старта ракет
.
Москва, Машиностроение, 2009, 448 с.
[3]
Власова Е.А., Зарубин В.С., Кувыркин Г.Н.
Приближенные методы мате-
матической физики
. Москва, Изд-во МГТУ им. Н.Э. Баумана, 2001, 700 с.
[4]
Banerjee P.K., Butterfield R.
Boundary Element Methods in Engineering Sci-
ence
. London, McGraw-Hill Book Company (UK) Limited, 1981, 494 p.
[5]
Brebbia C.A., Telles J.C.F., Wrobel L.C.
Boundary Element Techniques
. Berlin,
Springer-Verlag, 1984, 523 p.
[6]
Boundary Integral Equation Method: Computational Applications in Applied
Mechanics
. Ed. by Cruse T.A., Rizzo F.J. New York, ASME, 1975, 390 p.
[7]
Chuang Y.K., Ehrich O. On the Integral Technique for Spherical Growth Prob-
lems.
Int. J. Heat and Mass Transfer
, 1974, vol. 17, рp. 945–953.
[8]
Лойцянский Л.Г.
Механика жидкости и газа
. Москва, Наука, 1978, 736 с.
[9]
Соболев С.Л.
Уравнения математической физики
. Москва, Наука, 1966,
444 с.


