А.Л. Сушков
2
щего исправить сферическую аберрацию исходной линзы, которая
определяеется величиной коэффициента аберрации
S
I
. Деформация
первой сферической поверхности линзы в асферическую второго по-
рядка осуществляется введением в уравнение поверхности коэффи-
циента
b
1
, рассчитываемого по формуле
(
)
3
I 1
1
4
00
1
1
S r
b
n h
= −
−
,
(2)
где
S
I
— величина коэффициента сферической аберрации линзы;
r
1
,
h
1
— радиус кривизны и высота луча на первой поверхности линзы,
h
1
=
f '
;
n
00
—
показатель преломления стекла.
Для второй поверхности линзы коэффициент деформации
b
2
вы-
числяют по формуле
(
)
3
I 2
2
4
00
2
1
S r
b
n h
=
−
.
(3)
Однако асферизация поверхностей линз малого диаметра пред-
ставляет достаточно сложную технологическую задачу. Вместе с тем
технология изготовления и метрология высокоточных сферических
поверхностей в широком диапазоне диаметров линз достигли к концу
ХХ века высокого уровня.
Разработка теории аберраций GRIN ОС [2, 4, 5] и развитие техно-
логий неоднородных оптических сред, начавшееся с 1960-х годов, со-
здало предпосылки для конструирования GRIN-линз со сферическими
поверхностями и качеством аберрационной коррекции, соответству-
ющим качеству коррекции элемента с асферическими поверхностями.
В первую очередь это относится к исправлению сферической аберра-
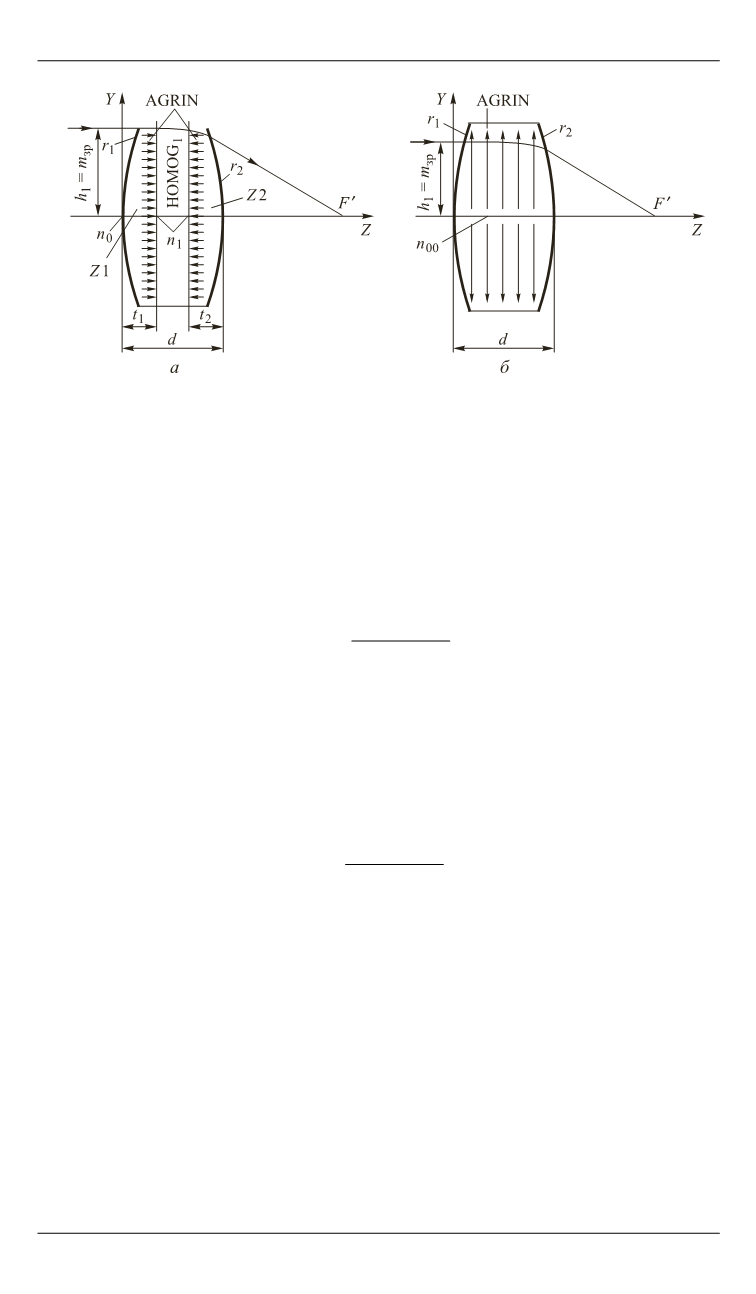
Параметры линзы с ОРПП (
а
) и РРПП (
б
)


