Неустойчивость Кельвина — Гельмгольца в сдвиговых течениях жидкости и плазмы - page 8

А.Ю. Чирков, В.И. Хвесюк
8
вающихся мод, распределенных по радиусу в пределах сдвигового
слоя. Поэтому при оценке коэффициента диффузии логично ориен-
тироваться на моды с δ⊥ ≈ 0,1L. Для таких мод kL ≈ 10, γ ≈ 0,1ω0, что
приводит к оценке коэффициента диффузии D ≈ 10–3V 0L. Полагая
D ≈ ν ≈ a, можно получить оценку турбулентного числа Рейнольдса
3
т 0 Re / 10 . V L ≈ ν ≈
Заключение. В гидродинамическом пределе кинетической не-
устойчивости Кельвина — Гельмгольца для плазмы волновое урав-
нение совпадает с уравнением Рэлея, описывающим течение идеаль-
ной жидкости. Для жидкости результат анализа устойчивости на ос-
нове уравнения Рэлея не всегда имеет физический смысл, так как в
ряде случаев, в частности вблизи стенок, пренебрежение молекуляр-
ной вязкостью некорректно [1]. В случае плазмы подход на основе
уравнения Рэлея применим для бесстолкновительных режимов. Кро-
ме того, плазма в магнитном поле изолирована от прямого контакта
со стенками, а профиль скорости бесконтактно формируется элек-
тромагнитными полями.
Характерный инкремент рассмотренной неустойчивости γ ≈
≈ 0,1V0/ L ≈ 0,1dV/dx . Инкремент такого же порядка характерен и для
случая неустойчивости сжимаемой вязкой жидкости [5]. Качествен-
ная картина неустойчивости сохраняется и в случае сжимаемой
плазмы в магнитном поле в приближении идеальной магнитной гид-
родинамики [6]. Вариации плотности, связанные с неустойчивостью
Кельвина — Гельмгольца, могут приводить к развитию вторичных
неустойчивостей гидродинамического типа [7], поэтому генерация
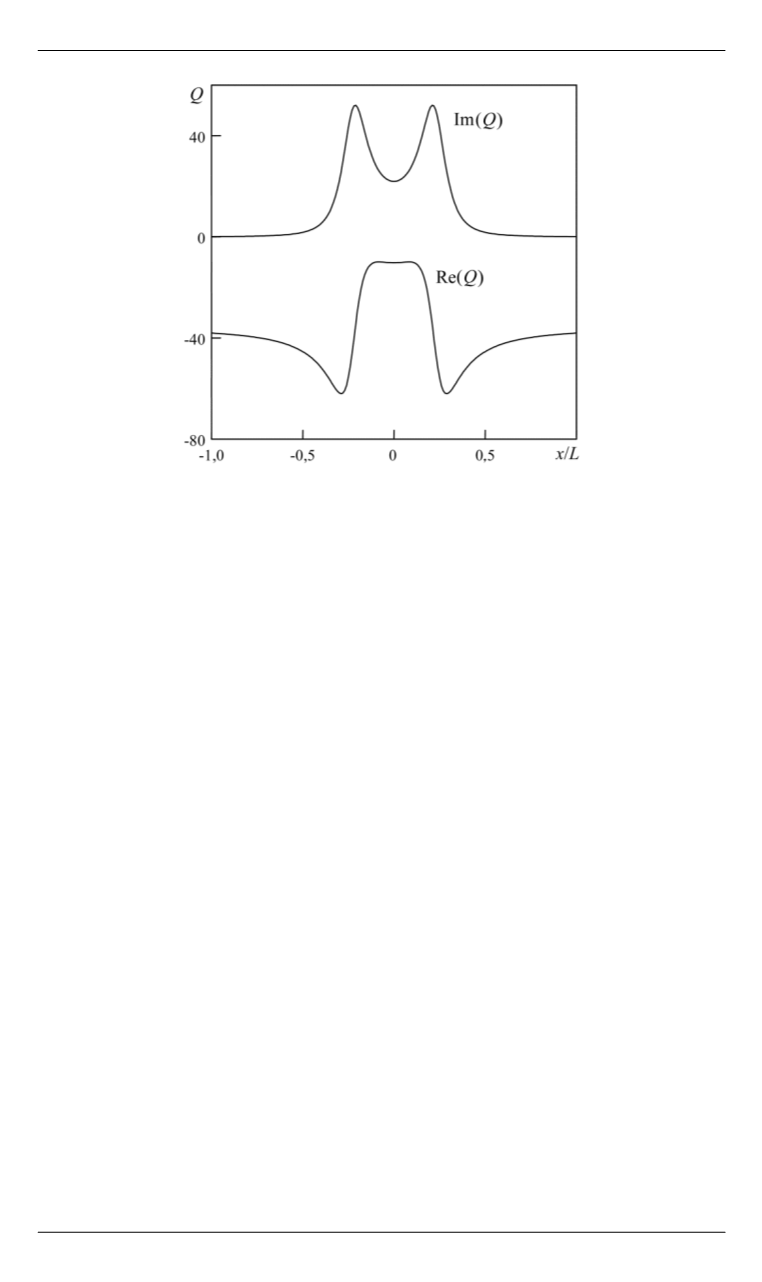
Рис. 9. Действительная и мнимая части функции Q для моды l = 0 при kL = 6