Неустойчивость Кельвина–Гельмгольца в сдвиговых течениях жидкости и плазмы
5
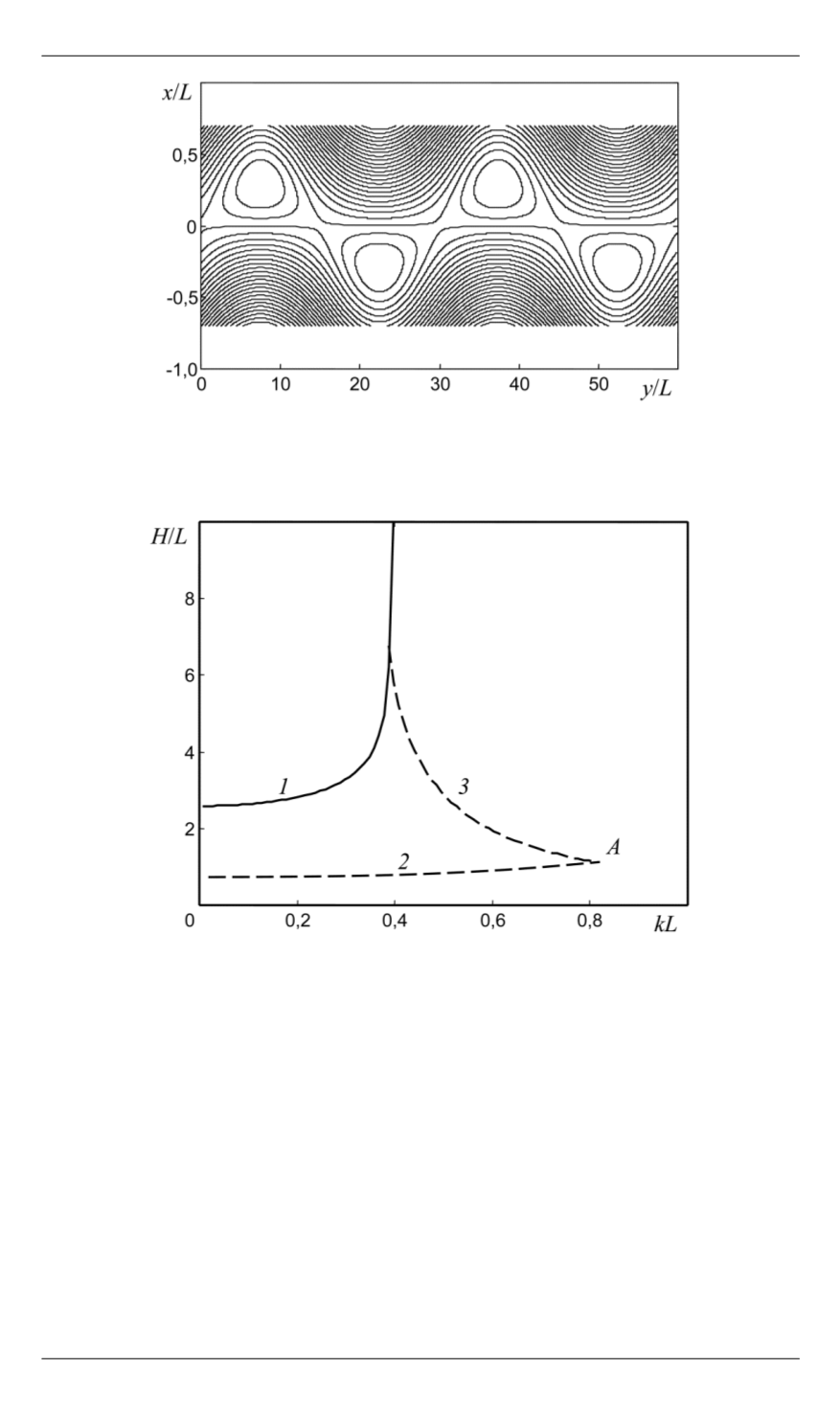
Рис. 4.
Вихри в области точки перегиба (
x
= 0) — линии уровня суммарной
функции тока
ψ
Σ
(
x
,
y
) моды с
kL
= 0,2 и
γ
/
ω
0
= 0,076. Для наглядности мак-
симальная амплитуда возмущенной скорости принята 0,5
V
0
Рис. 5.
Границы областей устойчивости мод, соответствующих граничным
условиям первого (
1
) и второго (
2
,
3
) родов, в потоке ограниченной шири-
ны
H
в зависимости от безразмерного волнового числа
kL
логична случаю неограниченного потока. Для рассматриваемых мод
можно установить границу устойчивости, т. е. такую ширину моды
H
, при которой
γ →
0. Отметим, что в данном численном алгоритме
невозможно использовать строгое равенство
γ
= 0, поэтому гранич-
ные кривые находят в результате приближения инкремента к нулю с
заданной точностью.
При рассмотрении граничных условий второго рода могут быть
найдены два нуля производной
d
ϕ
/
dx
(кривые
2
и
3
на рис. 5). Поло-
жение первого нуля производной (кривая
2
) практически не изменя-


