А.Ю. Чирков, В.И. Хвесюк
2
В результате линеаризации исходная система гидродинамических
уравнений сводится к уравнению Рэлея
2
2
2
2
2
/
0.
/
d
d V dx
k
dx
k V
⎛
⎞
ϕ + − +
ϕ =
⎜
⎟
ω −
⎝
⎠
(1)
Это уравнение с соответствующими граничными условиями со-
ставляет задачу о собственных функциях
ϕ
(
x
) и собственных значе-
ниях
ω
, в которой параметром является волновое число
k
моды. Ком-
поненты возмущенной скорости связаны с функцией
ϕ
(
x
) соотноше-
ниями:
( ) exp(
);
x
ik x
i t iky
= ϕ
− ω +
v
( / ) exp(
).
y
d dx
i t iky
= − ϕ
− ω +
v
Уравнение (1) для плазмы соответствует длинноволновому низ-
кочастотному пределу:
k
ρ
т
i
< 1; |
ω
| <<
ω
ci
, где
ρ
т
i
— циклотронный
радиус ионов, вычисляемый по ионной тепловой скорости;
ω
ci
—
циклотронная частота ионов.
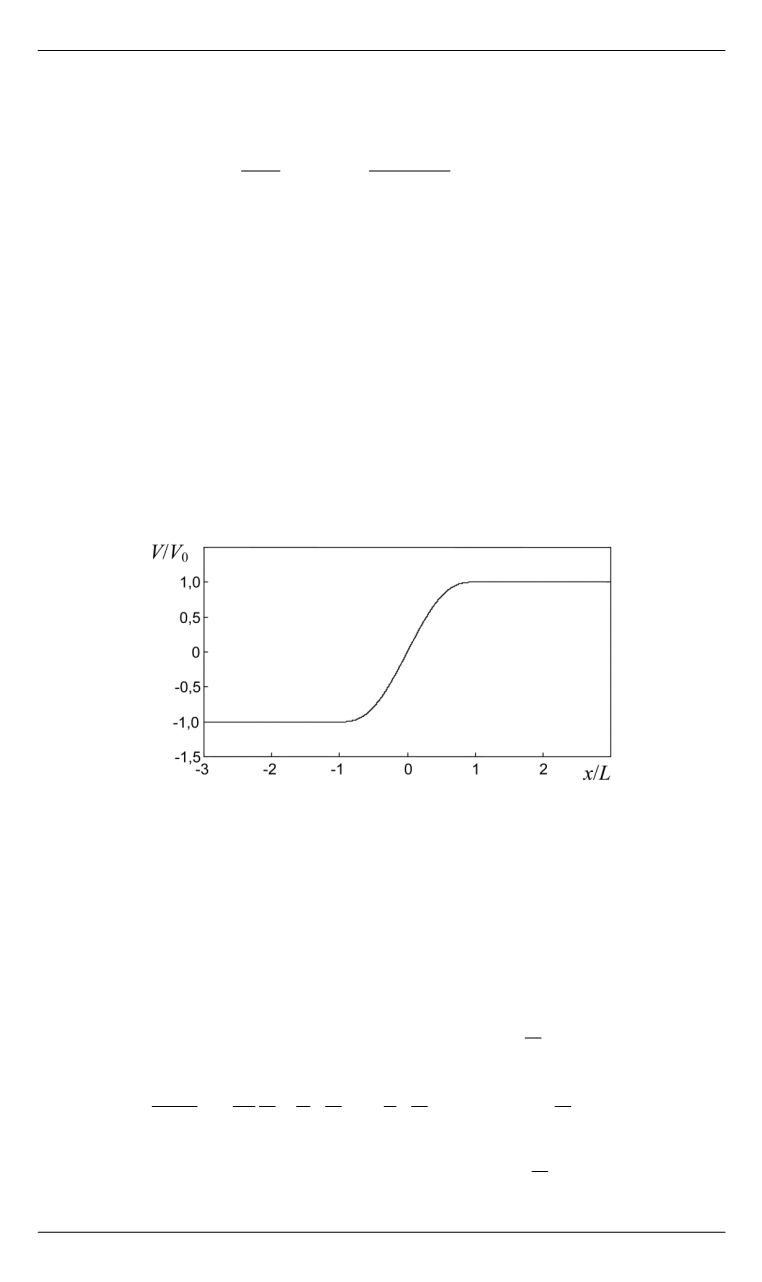
Нечетные моды.
Рассмотрим непрерывный профиль невозму-
щенной скорости
V
(
x
) с изменением в слое шириной 2
L
(рис. 1). Пер-
вая и вторая производные
V
(
x
) также непрерывны при любых
x
.
Начало отсчета координаты
x
выберем так, как показано на рис. 1,
что соответствует двум встречным потокам с одинаковыми скоро-
стями
V
0
. Аналитическое выражение для данного распределения ско-
рости имеет следующий вид:
3
5
0
1,
1;
( ) 15 5
3 ,
1
1;
8 4
8
1,
1.
x
L
V x
x
x
x
x
V
L L
L
L
x
L
⎧
−
< −
⎪
⎪
⎪
⎛ ⎞
⎛ ⎞
=
−
+
− ≤ ≤
⎨
⎜ ⎟
⎜ ⎟
⎝ ⎠
⎝ ⎠
⎪
⎪
>
⎪
⎩
(2)
Рис. 1.
Распределение скорости в системе со встречными потоками с пере-
ходным слоем шириной 2
L


