А.Ю. Чирков, В.И. Хвесюк
6
ется при увеличении инкремента, так как оно, по-видимому, опреде-
ляется структурой потока внутри переходного слоя. Область не-
устойчивости мод, соответствующих второму нулю производной,
находится над кривой
3
левее точки
A
.
Четные моды.
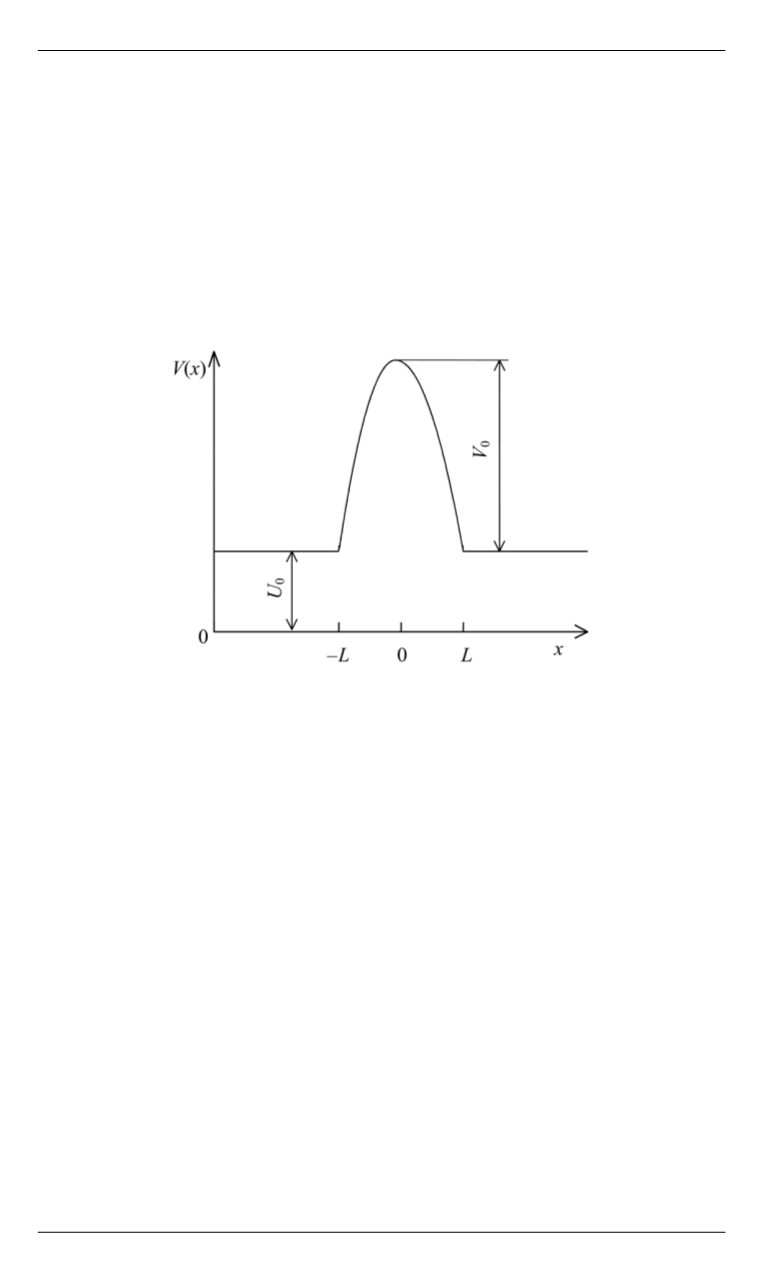
Для анализа четных мод рассмотрим распределе-
ние скорости потока, схематично показанное на рис. 6. Для решения
волнового уравнения (1) был использован ВКБ-метод. При этом для
каждого значения волнового числа
k
может быть определен набор
собственных частот
ω
l
(
l
= 0, 1, 2, … — номер моды) и соответству-
ющих собственных функций.
Рис. 6.
Четное распределение скорости течения
Результаты расчетов действительной частоты с учетом доплеров-
ского сдвига
0
0
Re(
)
R
kU kV
ω = ω− −
и инкремента
γ
= Im(
ω
) приве-
дены на рис. 7. В качестве масштаба частоты и инкремента, как и ра-
нее, принята величина
0 0
/ .
V L
ω =
На рис. 8 показаны радиальные профили мод, а на рис. 9 приве-
ден пример функции
Q
для действительных значений
x
. Согласно ре-
зультатам расчетов, при
kL
>> 1 точки поворота располагаются в глу-
бине слоя с неоднородностью толщиной 2
L
достаточно далеко от его
границ. По мере уменьшения параметра
kL
точки поворота прибли-
жаются к границам слоя, и существует такое значение (
kL
)
min
≈
1, при
котором точки поворота находятся на границе слоя, а при
kL
< (
kL
)
min
неустойчивость отсутствует. Для рассматриваемого распределения
скорости дрейфа
V
(
x
) инкремент максимален при
kL
= (
kL
)
min
, макси-
мальное значение инкремента
γ
max
≈ ω
0
.
Представленные на рис. 7 результаты соответствуют случаю, ко-
гда середина радиального профиля моды совпадает с центром слоя
(
x
= 0). Для мод, середины профилей которых смещены от точки
x
= 0
на величину
x
0
, значение (
kL
)
min
увеличивается, а
γ
max
уменьшается.


