Проектирование и комплексное математическое моделирование судна
9
менем расчета и точностью результатов. Учитывается конечная изгиб-
ная упругость оболочки, возвращающий момент пропорционален из-
менению двумерной кривизны поверхности, что позволяет, в частности,
учитывать ребра жесткости, локальные усиления в местах прикрепле-
ния тяг и т. п.
Для конуса граничные условия сверху задаются положением центра
нагнетателя (он же центр основания конуса, нагнетатель считаем пло-
ским) и ориентацией (два числа: например углы Эйлера). Поскольку
конус жестко связан с нагнетателем, положение его верхнего основания
относительного центра нагнетателя постоянно. Граничные условия
снизу обусловлены отсутствием составляющей силы изгиба, нормаль-
ной к границе.
Если расчетная поверхность на данном шаге «проникает» сквозь
рельеф, то в модели эта ее часть «укладывается» на рельеф. При этом
возникает и начинает действовать соответствующая сила трения.
Поверхность представляется в виде прямоугольной лагранжевой
сетки. Узлы соединены между собой ребрами. Узел (
i, j
) обладает мас-
сой
m
i,j
, элементарной площадью σ
i,j
. Коническая (вначале) поверхность
описывается
N
z
+ 1 слоями, каждый из которых состоит из
N
φ
узлов.
Самый верхний слой закреплен. Для описания поверхности требуется
N
φ
×
N
z
переменных.
Некоторые подпрограммы, реализующие указанные математиче-
ские модели частных аспектов функционирования ТСВП, писались на
С
++
и отлаживались отдельно. Они объединялись в комплексную мате-
матическую модель (рис. 4) путем автоматического создания общего
исходного файла на С
++
, включающего оптимизированные средства
решения дифференциальных уравнений (RADAU5 и др.). Учитывались
динамика движения ТСВП в целом, управление ТСВП, работа двига-
телей и трансмиссии, маршевые движители и рули, нагнетательный
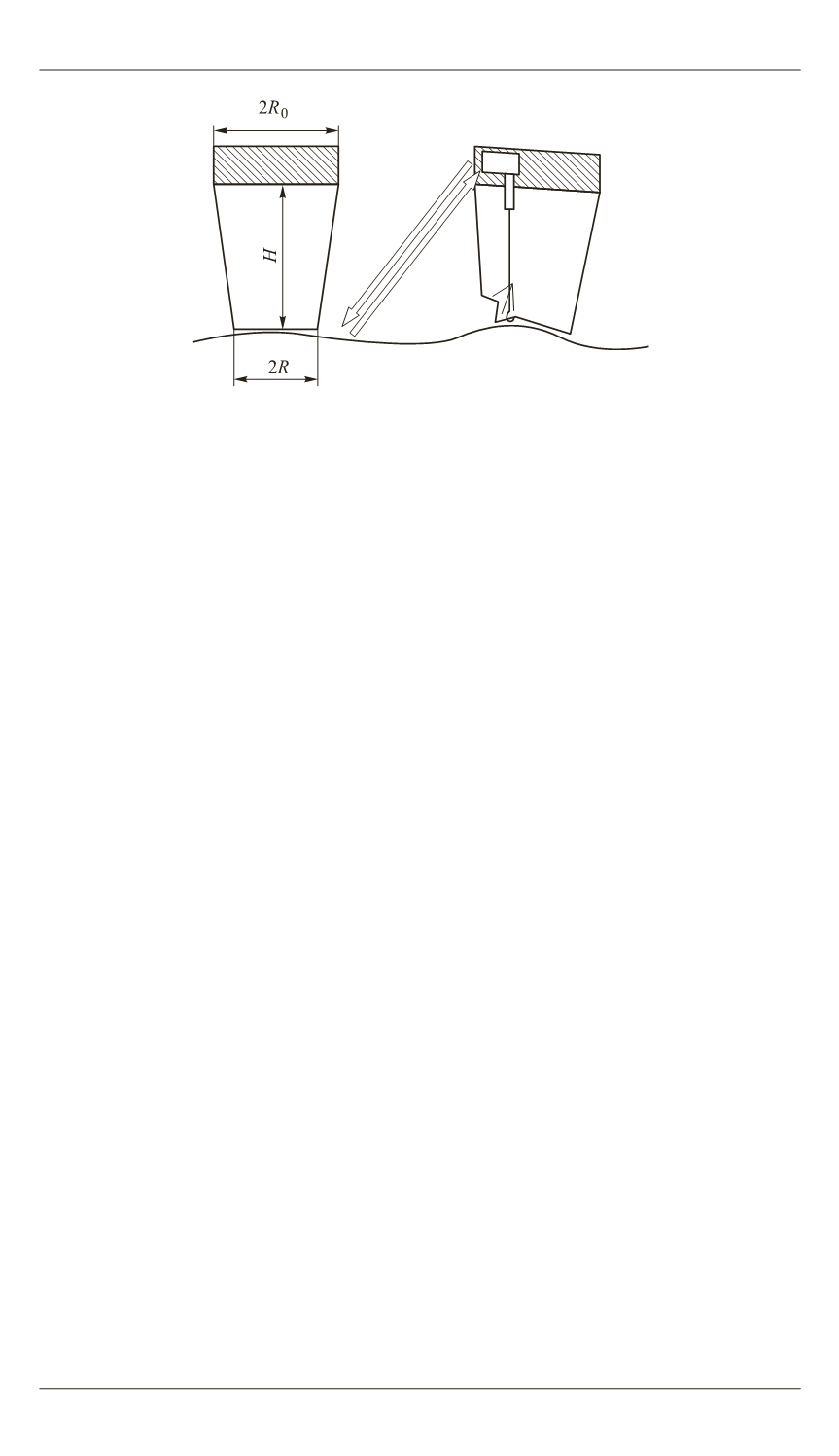
Рис. 3.
Схема управляемого ГО камерного типа, двигающегося по неров-
ной опорной поверхности


