
Определение траекторий космических объектов по оптическим измерениям
…
Инженерный журнал: наука и инновации
# 6·2017 3
где зона двойного обзора находится между
(
)
(1) (2)
н
1 1
max ,
t
t
t
=
и
(1) (2)
к
min ,
.
n m
t
t
t
Здесь
н
t
— время начала измерений;
к
t
— время их окончания.
Метод космической триангуляции предполагает определение ко-
ординат космического объекта одновременно с двух ИП-1 и ИП-2,
линейное расстояние между которыми (базис) известно с точностью
до сотых долей метра, а углы между базисом и направлениями на
объект определены ОЭС в один и тот же момент времени [9].
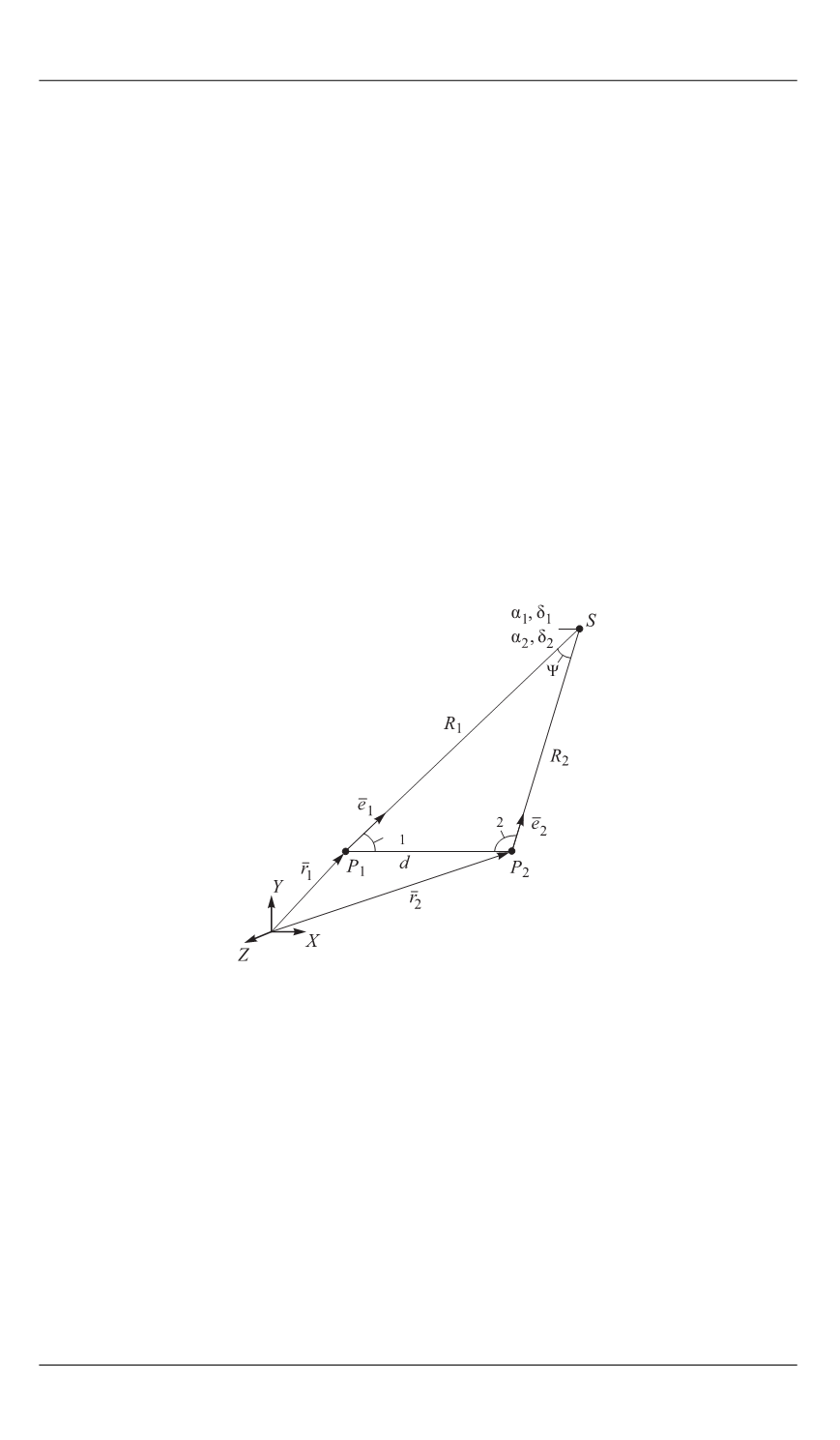
По известным значениям базиса и двух углов определяются сто-
роны треугольника, в вершине которого в некоторый момент време-
ни находится космический объект (рис. 1), что в конечном итоге поз-
воляет определить его координаты в фундаментальной инерциальной
системе координат (ФИСК). Важно отметить, что при расчетах учи-
тываются параметры вращения Земли, также влияющие на точность
решения задачи.
Рис. 1.
Плоский триангуляционный треугольник:
,
— углы соответственно прямого восхождения и склонения космического объекта;
—
угол между двумя направлениями на космический объект;
1
,
2
— углы между базой
d
и
направлением на космический объект;
X
,
Y
,
Z
— оси координат;
Р
1
,
Р
2
— точки нахождения
измерительных пунктов;
S
— положение космического объекта;
R
1
,
R
2
— дальности от изме-
рительного пункта до космического объекта;
r
1
,
r
2
— векторы положения измерительных
пунктов относительно центра системы координат;
1 2
,
e e
— единичные векторы направлений
на космический объект
Очевидно, что для использования метода космической триангу-
ляции необходимо обеспечить синхронность измерений. Для форми-
рования синхронных измерений следует представить информацию в
виде непрерывной функции времени.
ρ
ρ
















