
Методологические аспекты разработки математических моделей…
Инженерный журнал: наука и инновации
# 1·2017 3
Средняя абсолютная скорость
распространения фронта пламени
э
f
w
определяется по зависимости
э
отн
ос
,
f
f
w w w
= +
где
ос
w
— средняя скорость осе-
дания газовзвеси;
отн
f
w
— ско-
рость распространения фронта
пламени относительно неподвиж-
ной системы координат, связанной
с УПО.
Следует отметить, что экспери-
мент на данной установке проводи-
ли преимущественно при значениях
коэффициента избытка воздуха α <
< 0,5, поскольку при α ≥ 0,5 не реа-
лизуются достаточные для реги-
страции в УПО скорости распро-
странения фронта пламени в
газовзвесях большинства ПМГ. По-
следнее обстоятельство обусловли-
вает определенную специфику ис-
пользуемой математической модели,
так как, согласно данным [10], в
этом случае (при α < 1) необходимо
учитывать лучистый теплообмен.
Математическая модель.
Мо-
делирование распространения фронта пламени в газовзвеси ПМГ
условно можно разделить на три взаимозависимых этапа: 1) модели-
рование процессов, происходящих в газовой среде с учетом тепловы-
деления при горении частиц; 2) разрешение траекторной задачи для
частиц ПМГ; 3) моделирование лучистого переноса энергии.
При построении математической модели приняты следующие
допущения:
1) газовая среда представляет собой смесь воздуха и продуктов
сгорания ПМГ;
2) при взаимодействии ПМГ с воздухом конденсированные про-
дукты реакции накапливаются в пределах фронта пламени частицы;
3) газовая среда оптически прозрачна;
4) частицы ПМГ имеют сферическую форму;
5) особенности геометрии расчетной области допускают двумер-
ную постановку задачи.
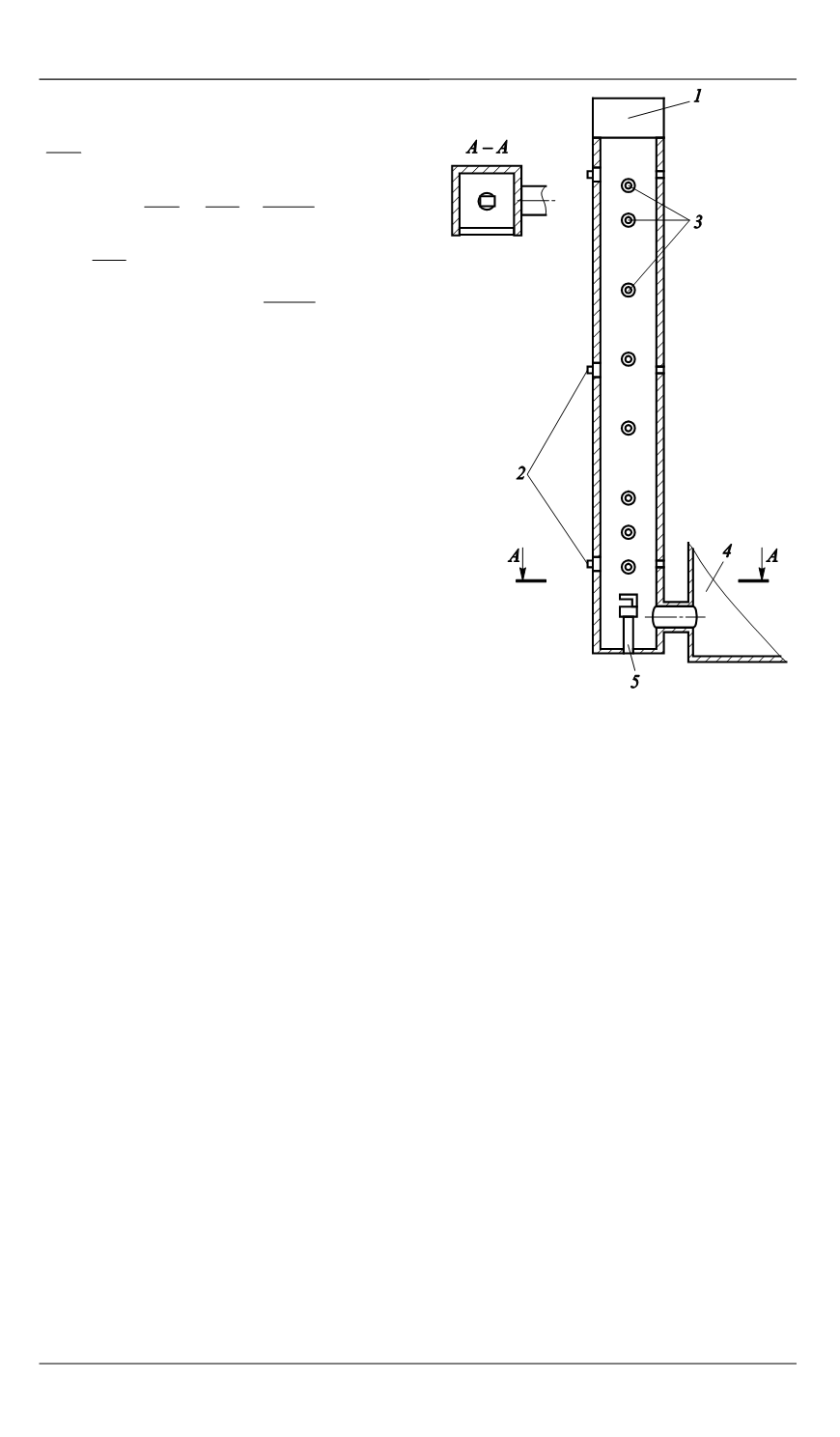
Рис. 1.
Схема рабочего участка
«УПО 1500»:
1
— устройство распыливания ПМГ;
2
—
датчики регистрации оседания ПМГ;
3
—
датчики регистрации перемещения фронта
пламени;
4
— газовые ресиверы;
5
— вос-
пламенитель


















