
В.М. Дубровин, Т.А. Бутина
2
Инженерный журнал: наука и инновации
# 11·2016
том, что в данном случае определяется деформативность самого
упругого заполнителя. Предполагается, что материал заполнителя
удовлетворяет основным соотношениям теории упругости, а упругие
характеристики заполнителя при динамическом нагружении соответ-
ствуют характеристикам при статическом нагружении [5–7].
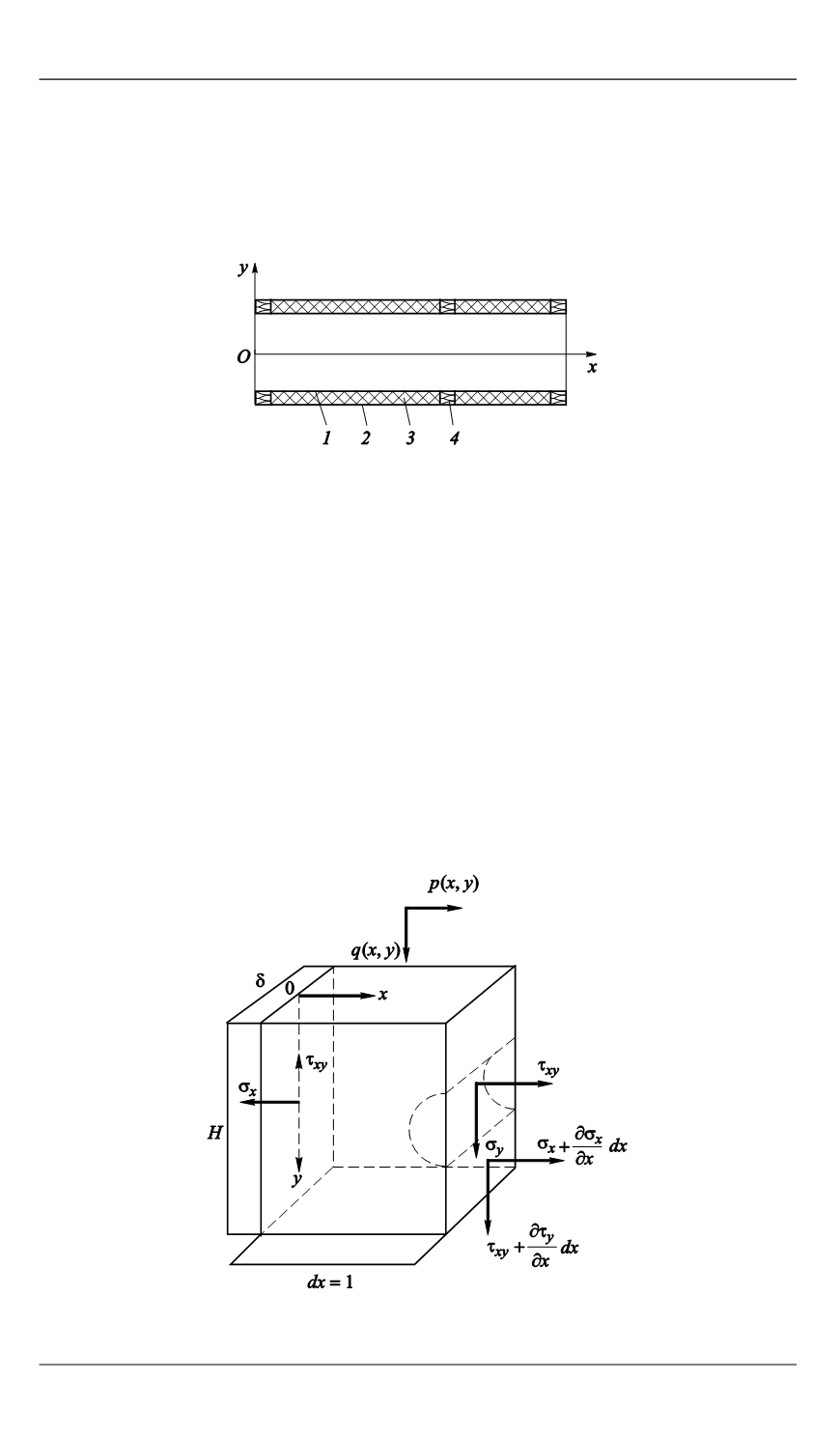
Рис. 1.
Конструктивная схема составной
оболочки с упругим основанием:
1
,
2
— внутренняя и внешняя оболочки;
3
—
упругое основание;
4
— дискретная упругая
опора
Выделим по образующей оболочки элементарную полоску ши-
риной
,
δ
предполагая, что вследствие малости
1
δ
кривизной полоски
можно пренебречь. Поперечными сечениями выделим участок еди-
ничной длины
1.
dx
=
Рассмотрим равновесие выделенного элемента
(рис. 2). Задача определения деформации выделенного элемента сво-
дится к плоской задаче теории упругости, так как любой из участков
выделенной длины находится в одинаковых условиях и работает ана-
логично соседним участкам.
Рис. 2.
Схема сил и моментов, действующих на элемент упругого основания
















