
А.Г. Андреев, Г.В. Казаков, В.В. Корянов
10
Инженерный журнал: наука и инновации
# 6·2016
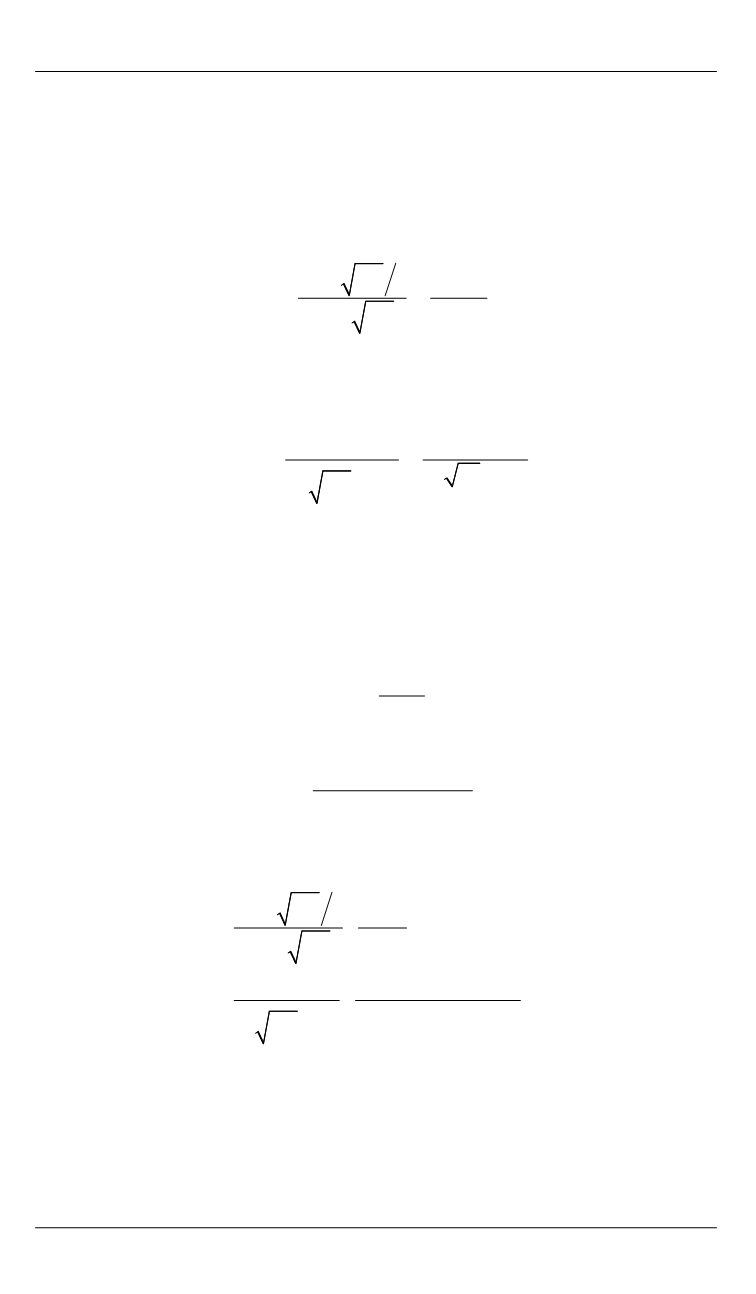
1
Д
=
Е
[Д
1
K
3
+ 0,5] =
Е
[2
0,256 + 0,5] = 1;
1
1
1
П И Д
= 16 – 1 = 15,
где
Е
[
] — операция округления до большего целого.
1.5. Определяем минимаксную оценку показателя надежности
ПО АСУ КА по результатам первого этапа испытаний:
1
1
ММ
1
1
П И 2 15 2 0,85.
16 4
И И
Р
2. Вычисляем оценку показателя надежности ПО АСУ КА по ре-
зультатам двух этапов испытаний.
2.1. Находим дисперсию минимаксной оценки:
2
2
1
ММ ММ
1
1
(
)
0, 01.
4( 16 1)
4 И 1
D Р
2.2. Полагаем, что оценка показателя надежности ПО АСУ КА
распределена по закону бета-распределения с параметрами
а
и
b
, и
составляем систему уравнений для определения этих параметров.
Математическое ожидание случайной величины, распределенной
по закону бета-распределения с параметрами
а
и
b
,
МО ,
а
а b
а дисперсия
2
.
(
) (
1)
аb
D
а b а b
Следовательно, система уравнений имеет вид
1
1
1
1
2
2
1
П И 2
,
И И
1
.
(
) (
1)
4 И 1
а
а b
аb
а b а b
(9)
2.3. Вычисляем оценки параметров
а
*
и
b
*
как решение системы
уравнений (9). В результате получаем
















