
Цифровой фильтр для подавления влияния…
13
Дифференциальное уравнение (7) было решено в среде Mathe-matica
Wolfram Research c использованием функции NDSolve. На рис. 16
представлена реакция фильтра при подаче на вход сигнала
x
(
t
) =
sin(2π
ft
) с различными частотами в полосе подавления. Амплитуда
выходного сигнала
y
(
t
) в точности совпадает со значениями АЧХ для
данных частот, неустойчивости не наблюдается.
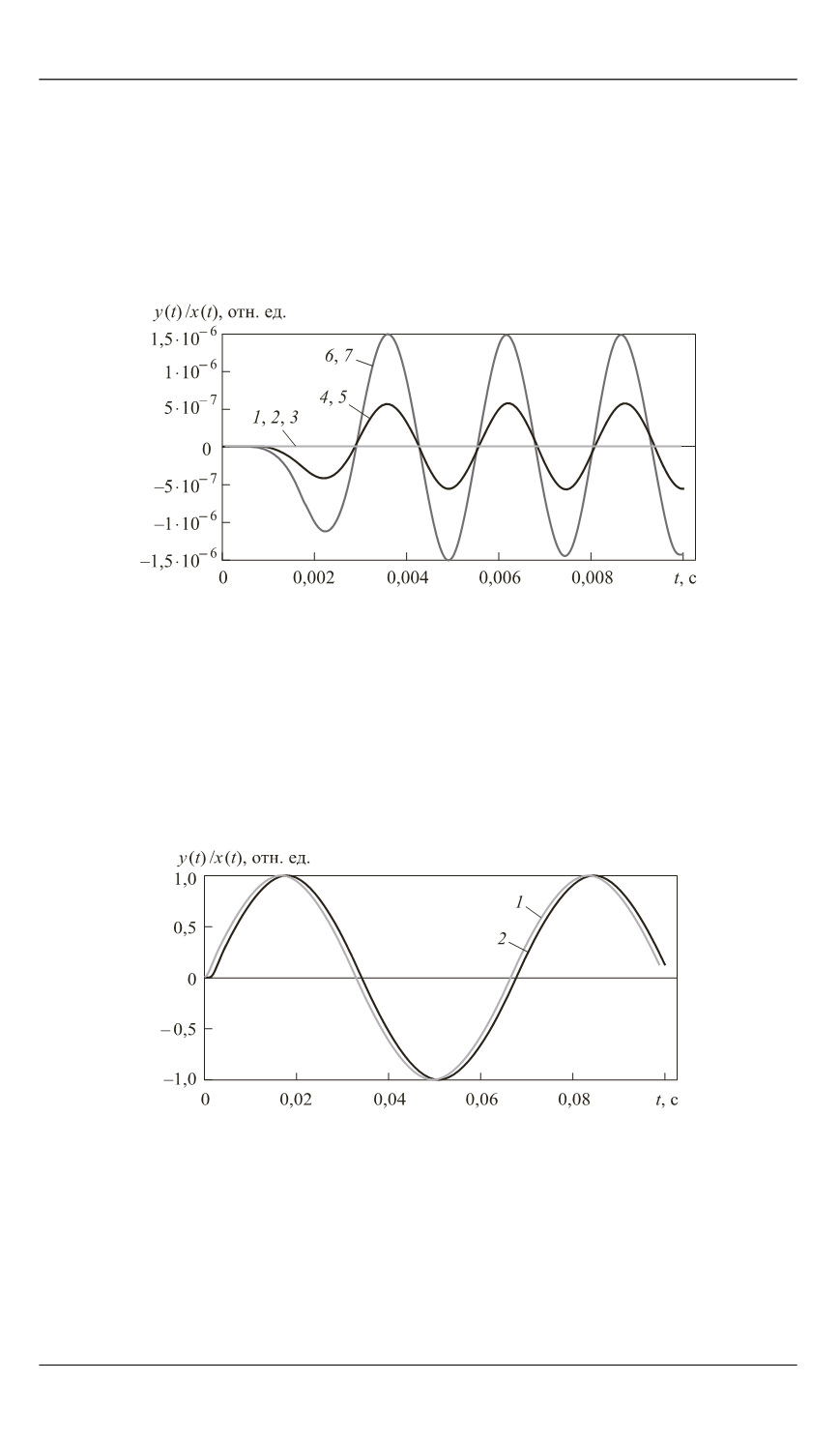
Рис. 16.
Выходной сигнал
y
(
t
) для
x
(
t
) = sin(2π
ft
) при различ-
ных значениях
f
:
400 – 2,25 Гц (
1
); 400 Гц (
2
); 400 + 2,25 Гц (
3
); 400 – 1,3 Гц (
4
);
400 + 1,3 Гц (
5
); 397 Гц (
6
); 403 Гц (
7
)
Для определения задержки сигнала на частоте 15 Гц (правая гра-
ница диапазона пропускания) подадим на вход фильтра сигнал
x
(
t
) = sin(2π·15
t
) (рис. 17).
Рис. 17.
Задержка выходного сигнала на частоте 15 Гц
на границе полосы пропускания:
1
— входной сигнал
x
(
t
) = sin(2π·15
t
);
2
— выходной сигнал
y
(
t
)
Анализируя зависимости, приведенные на рис. 17, видим, что
время задержки выходного сигнала
y
(
t
) по отношению к входному
x
(
t
) не более 0,0014 с, что меньше допустимого времени задержки
0,1·0,5/15, равного 0,0033 с.

















