
В.И. Рязанцев, А.С. Дьяков
4
Вторым будем считать участок, расположенный после нелинейного
элемента и включающий в себя первый участок и следующий за ним блок
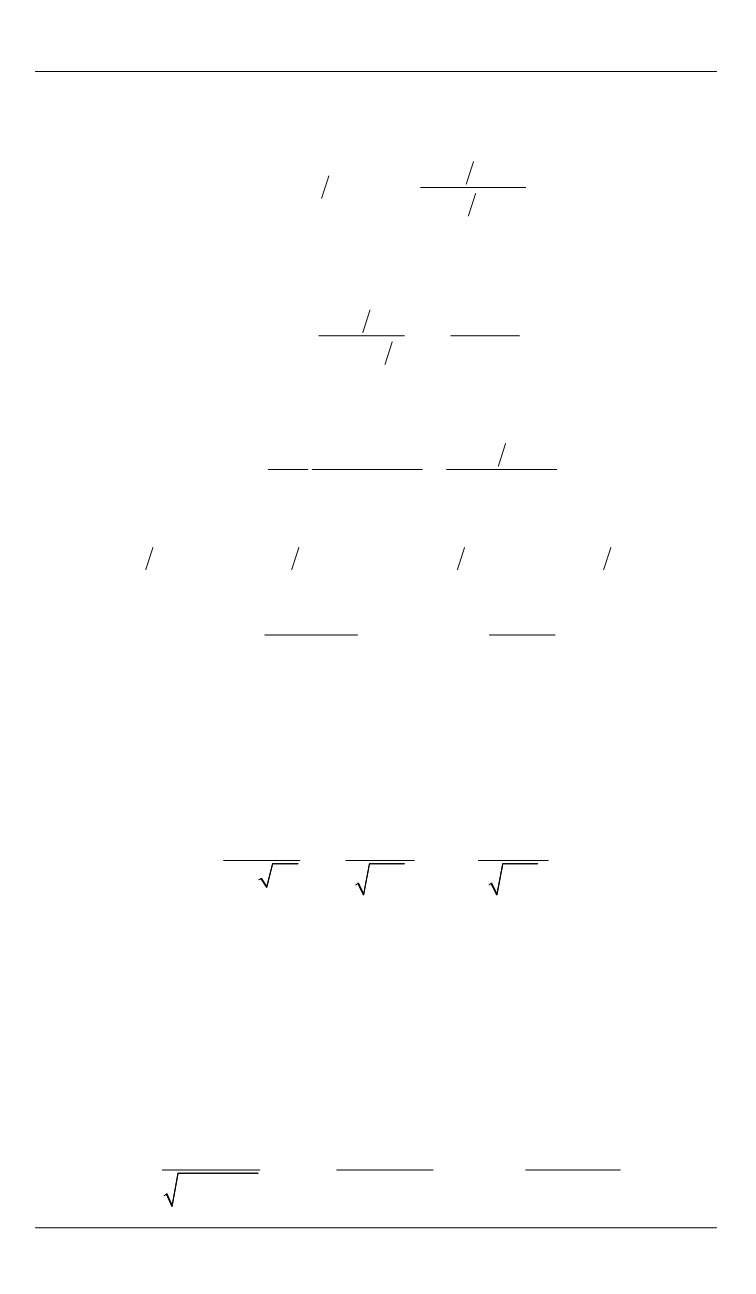
интегрирования. В этом случае передаточная функция
2
1
1
( ) (1 ) ( )
.
1
k
W s
s W s
s ms k
Для третьего участка, расположенного непосредственно перед нели-
нейным элементом и состоящего из блоков интегрирования и обратной
связи, передаточная функция определяется так:
a
a
3
2
2
a 3
a 3
( )
,
1
v s
v
W s c
c
v c s
s v c
где
2 3
,
c c
— коэффициенты;
a
v
— скорость автомобиля.
Преобразуем полученное выражение:
a 2
2 3
3
1
1
a 3
3
3
1
( )
(
)
1 (
)
1
a
a
v c
c c
W s
v c v c s
v c s
и сделаем замену переменных:
2
1 ;
h k
2
;
H m k
3 2 3
;
h c c
3
3
1 .
a
H v c
В результате получим
2
2
2
( )
;
(
1)
h
W s
s H s
3
3
3
( )
.
1
h
W s
H s
На рис. 3,
б
изображена структурная схема АСУС, эквивалентная ис-
ходной. Найдем для этой системы коэффициенты статистической линеари-
зации нелинейного звена.
При замене нелинейного элемента линейным коэффициент статистиче-
ской линеаризации по неслучайной составляющей определяется выражением
к
к
к
к
к
0
0
,
2
y
y
y
y
y
m d
m d
F K
m
D
D
где
к
,
y
m
к
y
D
математическое ожидание и дисперсия поперечной де-
формации колеса
к
у
соответственно; Ф
интеграл Лапласа.
Коэффициенты линеаризации по случайной составляющей представим
в двух формах в зависимости от условий их получения.
В работах [9, 10] в качестве критерия статистической эквивалентности
принимают равенство математических ожиданий и дисперсий случайного
процесса на выходе нелинейного и линейного элементов.
В этом случае коэффициент
к
к
к
к
к
2
2
(1)
0
1
(
)
(
)
exp
exp
.
2
2
2
y
y
y
y
y
d m
d m
F
K
D
D
D

















