
Нелинейная система управления схождением колес автомобиля
3
Сравнение процессов изменения длины поперечной тяги в линейной и не-
линейной системах регулирования показывает, что при соответствующим об-
разом подобранных параметрах системы
передаточных коэффициентах,
определяемых параметрами линейных усилителей,
эти процессы являются
достаточно близкими (незначительные отличия наблюдаются только в первые
секунды движения). Поэтому во многих задачах по устойчивости движения
автомобиля с АСУС таким расхождением можно пренебречь.
Аналогичное преобразование можно применить в задачах, связанных с
работой АСУС в области случайных процессов. Реальные приводы управле-
ния, выполняемые на базе гидравлических элементов, обеспечивают чаще все-
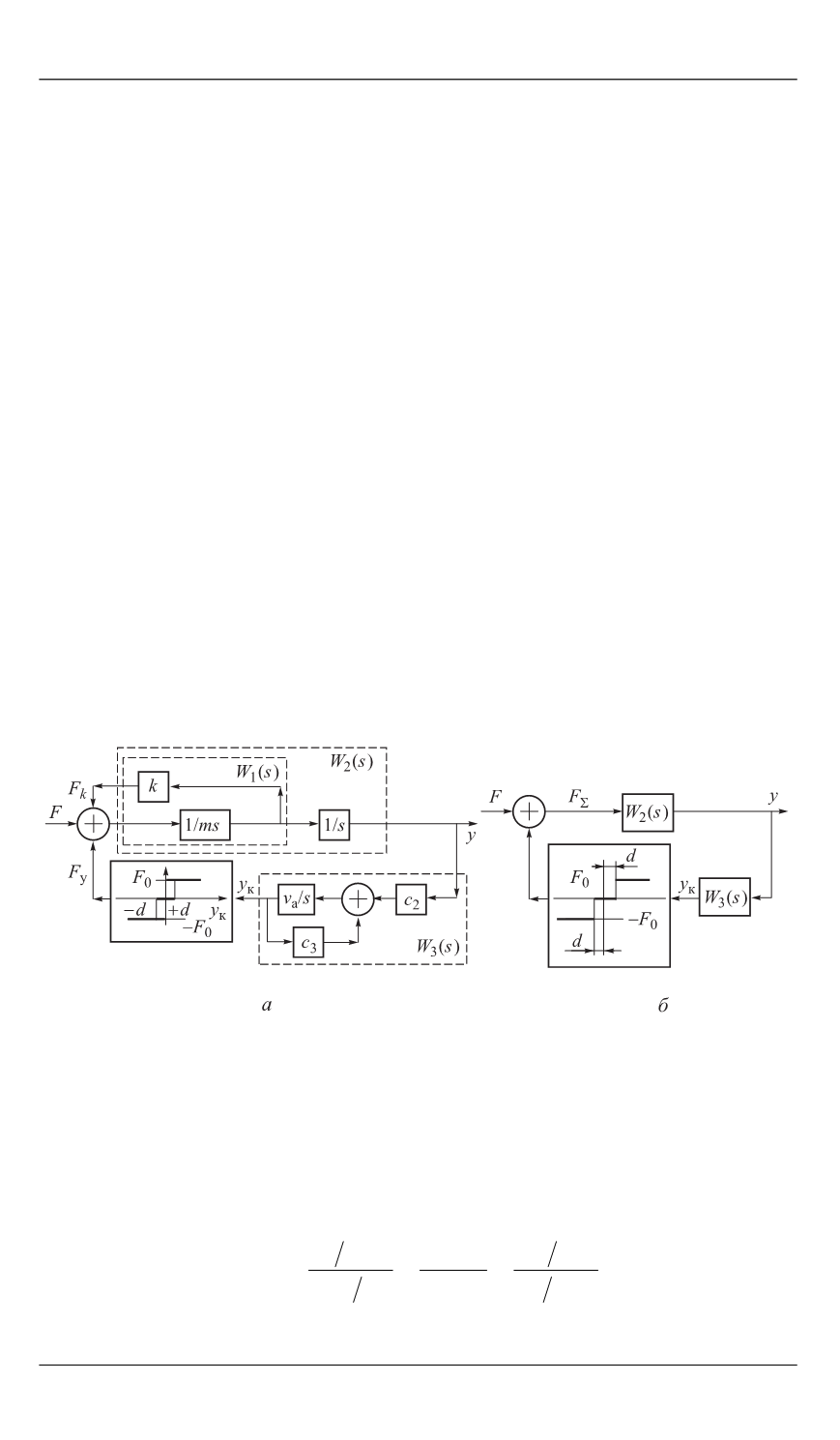
го нелинейную силовую характеристику. В качестве примера рассмотрим
структурную схему, изображенную на рис. 3. Здесь функция
упр к
( )
F y
характеризуется зоной нечувствительности при значениях аргумента
к
y
от
−
d
до +
d
(в данном случае
к
y
боковое перемещение ступицы колеса
относительно центра пятна контакта) и постоянным значением функции
упр
F
при остальных значениях аргумента.
Прямое решение нелинейной АСУС аналитическими методами невоз-
можно, поэтому приведем систему к виду, позволяющему получить реше-
ние [9, 10]. В соответствии с этим методом в исходной структурной схеме
АСУС выделим участки
W
1
(
s
),
W
2
(
s
) и
W
3
(
s
) до и после нелинейного эле-
мента и запишем соответствующие им передаточные функции.
Рис. 3.
Структурные схемы исходной АСУС (
а
) и эквивалетной ей (
б
)
Для первого участка (после нелинейного элемента), содержащего блок
деления на
m
, блок интегрирования, а также блок обратной связи (коэффи-
циент
k
) передаточная функция имеет вид
1
1
1
1
( )
,
1
1
ms
k
W s
k ms ms k ms k
где
m
масса подвижных частей привода;
s
оператор Лапласа.

















