
В.Г. Богомолов, А.А. Федотов
4
Уравнения движения недеформируемой части правой половины
крыла 2 представлены формулами (1) при изменении лагранжевой
координаты
2
s
a
от
0
до
2
0
a
,
2
0
2 3
a
. Параметр
2
0
a
— лагранжева
координата сечения крыла 2, отделяющая недеформируемую часть
крыла от деформируемой.
Уравнения движения деформируемой части правой половины
крыла 2 в безразмерной форме записываются в виде
1
1
2
0
0
(
) cos ( )
( ) 1 cos ( , ) sin ( ),
s
s
s
x a b
t b r t
a t
t
2
2
2
0
( ) sin ( , )
,
s
s
x r t
a t a
(2)
3
1
2
0
(
) sin ( ) cos ( ) ( ) 1 cos ( , ) cos ( ),
s
s
s
x a b
t h
t r t
a t
t
где
1
0
1;
s
a
2 2
0
1;
s
a a
2
0
2 3;
a
( ) ( ) ( );
t
t
t
2 2
2
0
2
0
( , ) ( )
;
1
s
s
a a
a t
t
a
0
( )
,
sin ( )
r
r t
t
причем
( ) arctg ( sin ( ));
t
h
t
0
( )
sin ( );
t
t
0
( )
sin ( ),
t
t
0
1,
2
0 0
0
(1 ),
r
l
a
2.
l
Наряду с неподвижной системой координат введем в рассмотрение
подвижную систему
1 2 3
O y y y
, жестко связанную с крылом (рис. 2).
Ось
2
y
параллельна оси
2
x
, ось
1
y
направлена вдоль корневой хорды
AB
(см. рис. 1), а начало системы координат
1 2 3
O y y y
совпадает с точ-
кой
O
— проекцией оси угловых колебаний на плоскость
2
0
x
.
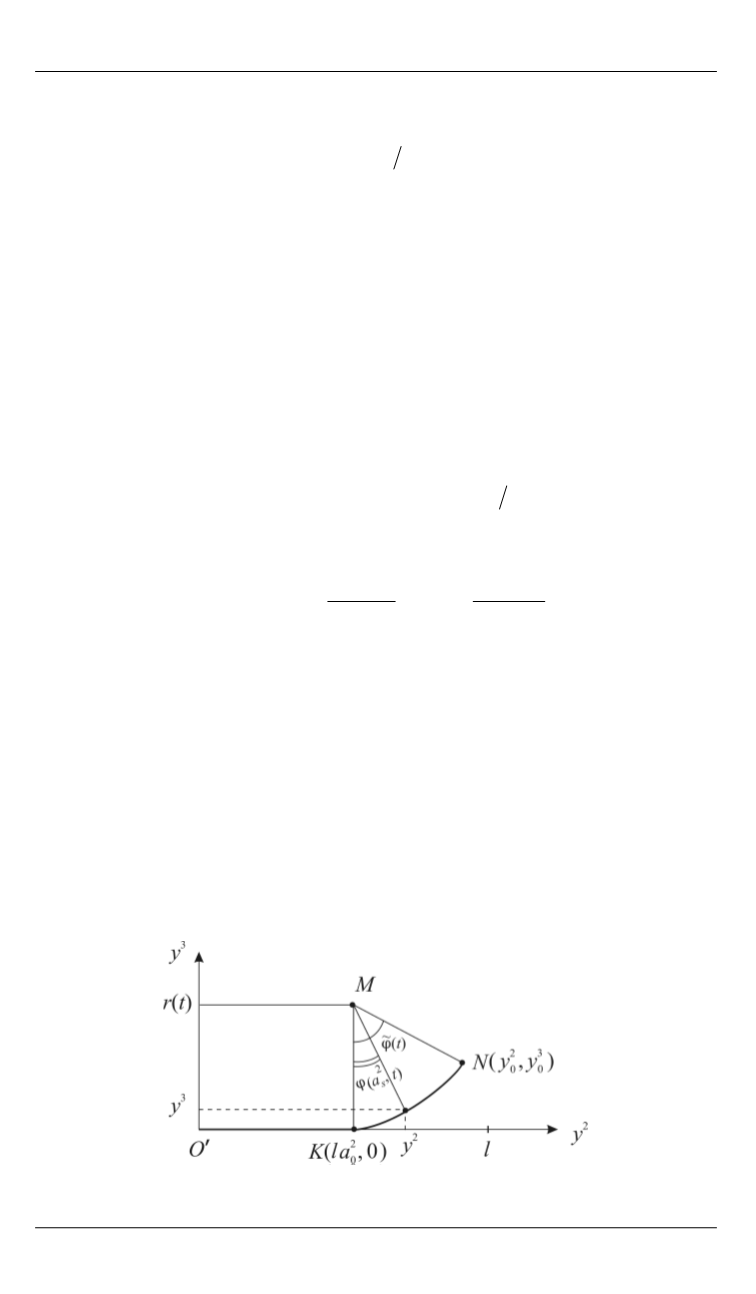
Рис. 2.
Крыло 2 в системе координат
1 2 3
O y y y

















