
В.Г. Богомолов, А.А. Федотов
2
ные направлению основного движения периодические колебания с
амплитудами порядка поперечных размеров своего тела. При этом
центр масс тела дельфина практически движется равномерно и пря-
молинейно. Траектория движения точки развилки хвостового плав-
ника близка к синусоиде [5].
Закон движения модели хвостового плавника.
Введем в рас-
смотрение неподвижную прямоугольную декартову систему коорди-
нат
1 2 3
, ,
x x x
. Поток на бесконечности будем считать однородным с
постоянным вектором скорости
V
, параллельным оси
1
x
и направ-
ленным в положительную сторону этой оси. Хвостовой плавник
дельфина будем моделировать тонким н е д еформиру емым плос-
ким крылом прямоугольной формы в плане (крыло 1) и тонким
д ефо рмиру емым крылом (крыло 2).
Полагаем, что крыло 1 совершает периодические угловые коле-
бания вокруг горизонтальной оси, фиксированной в плоскости крыла
параллельно прямолинейной задней кромке. В свою очередь ось уг-
ловых колебаний, расположенная поперек направления основного
движения, совершает вертикальные гармонические колебания, оста-
ваясь параллельной самой себе. Движение крыла удобнее описать в
системе координат
1 2 3
,
,
x x x
(рис. 1), в которой жидкость на беско-
нечности покоится и оси которой параллельны соответствующим
осям системы
1 2 3
, ,
x x x
.
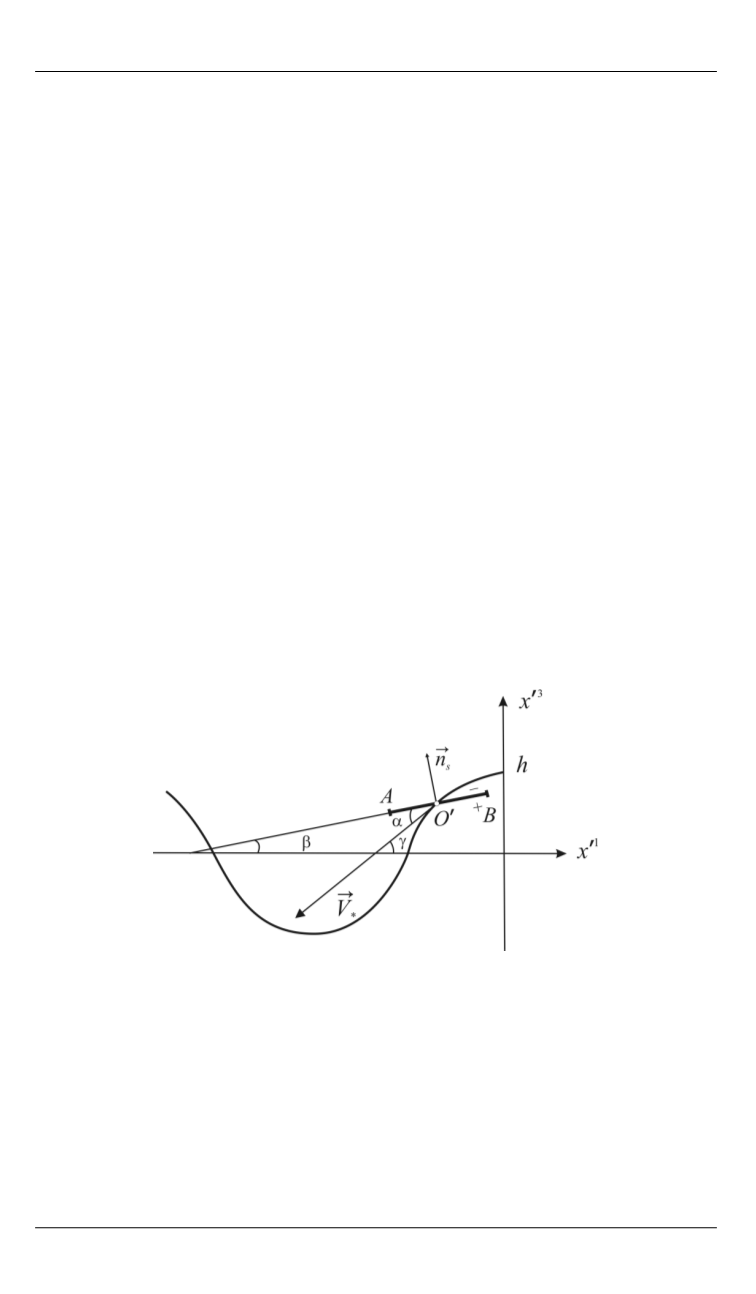
Рис. 1.
Крыло 1 в системе координат
1 2 3
Ox x x
Ось угловых колебаний, параллельная оси
2
x
, движется вдоль
вертикальной оси по гармоническому закону
3
cos ( )
x h
t
, а вдоль
горизонтальной оси — по закону
1
x
t
. Крыло проецируется на
плоскость
1 3
x x
только корневой хордой
AB
, ось угловых колеба-
ний — точкой
O
. Таким образом, положение крыла в каждый мо-

















