Окар Мин, Д.В. Мельников
6
Рис. 6.
Вычисление матрицы умножения в базисе функций Уолша
Этап. 6
. Проверка выполнения критерия (4) или (5). Если мини-
мум найден, то при соответствующих параметрах проводим анализ
системы, в противном случае переходим к этапу 3, т. е. присваиваем
искомым параметрам
1
j
p
значения в соответствии с выбранным ал-
горитмом минимизации целевой функции (функции многих перемен-
ных).
Для рассматриваемого примера за 14 итераций были найдены
следующие параметры:
*
ус
468,9355;
K
*
ф1
1288,0187;
T
*
ф2
0,1501;
T
* * *
ус ф1 ф2
,
,
0,8982.
J K T T
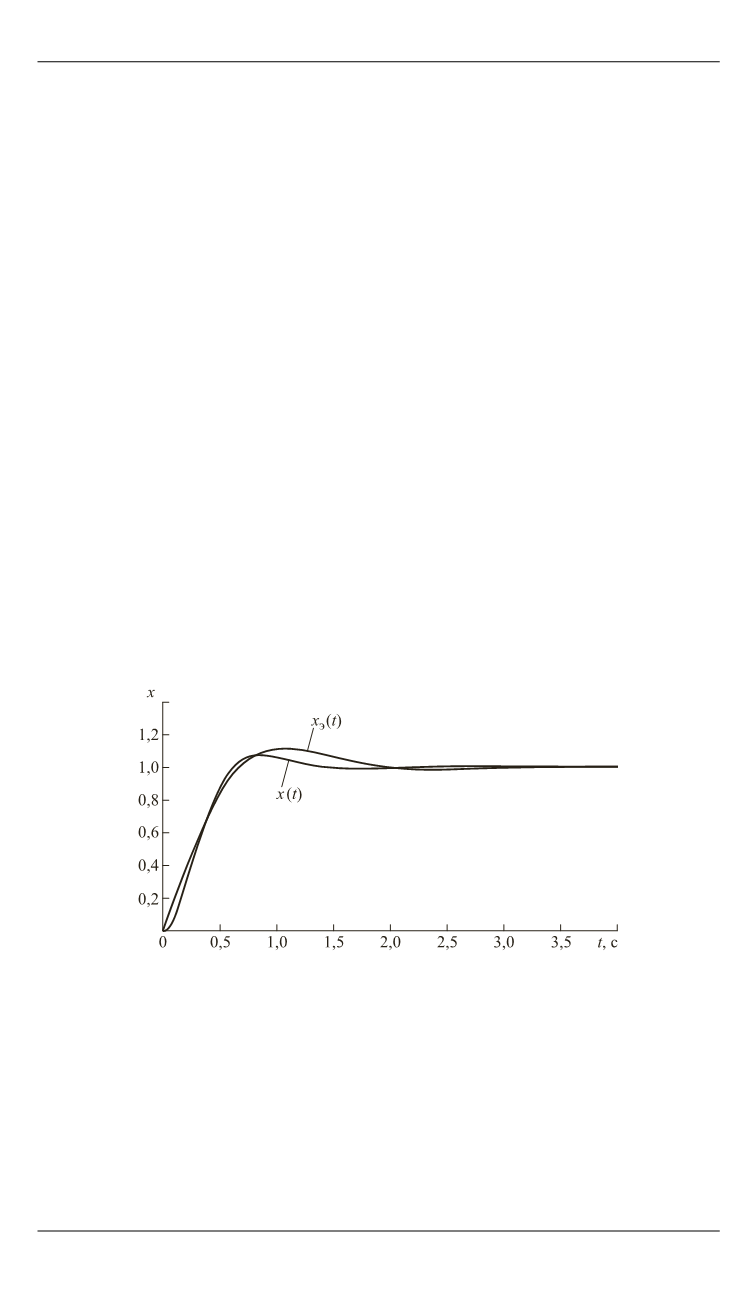
На рис. 7 представлены реальный
x t
и эталонный
э
x t
пере-
ходные процессы.
Рис. 7.
Переходные процессы радиоэлектронной системы
автоматического управления
Для предложенного алгоритма синтеза характерно следующее. Ал-
горитм применим для исследования и синтеза регуляторов в классе ли-
нейных и нелинейных нестационарных систем и не требует нахождения
дифференциального уравнения системы, связывающего входной и вы-
ходной процессы. Что касается сложных автоматических систем,
например класса нестационарных систем высокого порядка, то задача
построения уравнения вход-выход чрезвычайно трудоемка, требует
function Ay=m_ymn(H,f)
% Матрица умножения в базисе функций Уолша, упорядоченных по Адамару
% операция умножения на некоторую функцию f — вектор-столбец
% H-матрица Адамара
Ay=H*(H.*kron(ones(1,length(f)),f));


