Алгоритм расчета нелинейных систем управления проекционно-матричным методом
3
Реле описывается следующей зависимостью:
р ф2
р р ф2
ф2
ф2
ф2
,
1, 2;
1, 2,
1, 2;
1, 2,
1, 2.
x x
x F x
x
x
x
(2)
Задача состоит в расчете параметров фильтров
ф1
T
,
ф2
T
и усили-
теля сигнала
ус
K
таким образом, чтобы при подаче команды управ-
ления в виде единичной ступеньки переходный процесс
x t
систе-
мы приближался бы к некоторому желаемому (эталонному) процес-
су. Зададим эталонный выходной процесс в виде
1,8
э
1
cos 2, 3 .
t
x t
e
t
(3)
Алгоритм проекционно-матричного метода синтеза систем
управления основан на представлении процессов в форме разложения
по базисной системе функций. Такой подход позволяет перейти к
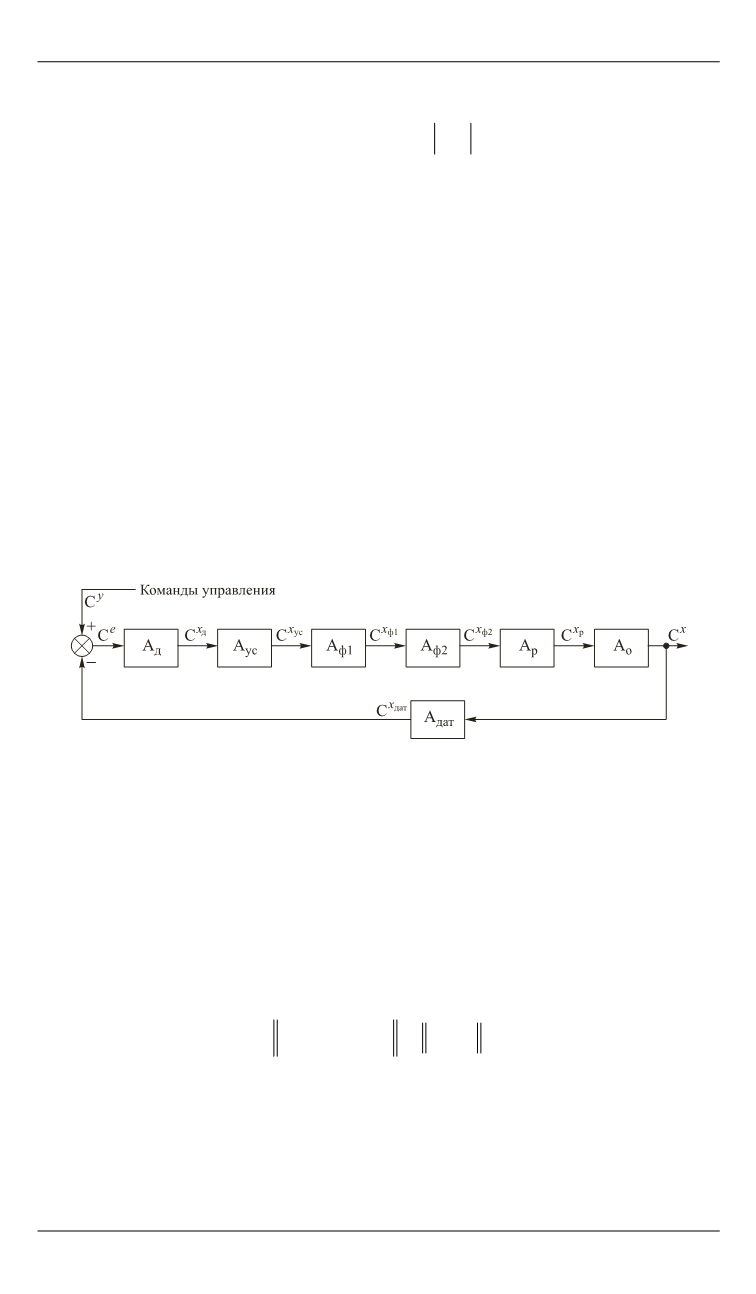
операторной форме представления системы рис. 3 [2, 3].
Рис. 3.
Операторная форма радиоэлектронной системы
автоматического управления
На рис. 3 обозначено:
д
,
A
ус
,
A
ф1
,
A
ф2
,
A
р
,
A
o
,
A
дат
A
—
матричные операторы соответствующих звеньев;
,
y
С
,
e
С
д
,
x
С
ус
,
x
C
ф1
,
x
C
ф2
,
x
C
р
,
x
C
,
x
C
дат
x
C
— спектральные характеристики соответ-
ствующих процессов.
С учетом такого операторного представления системы меру бли-
зости эталонного и реального переходных процессов можно записать
в терминах матричных операторов:
э
min,
x
x
J
p
p C p C E p
(4)
где
T
ф1 ф2 ус
,
,
T T K
p
— вектор искомых параметров;
x
C p
– спек-
тральная характеристика реального переходного процесса;
э
x
C
— спек-
тральная характеристика эталонного переходного процесса.


