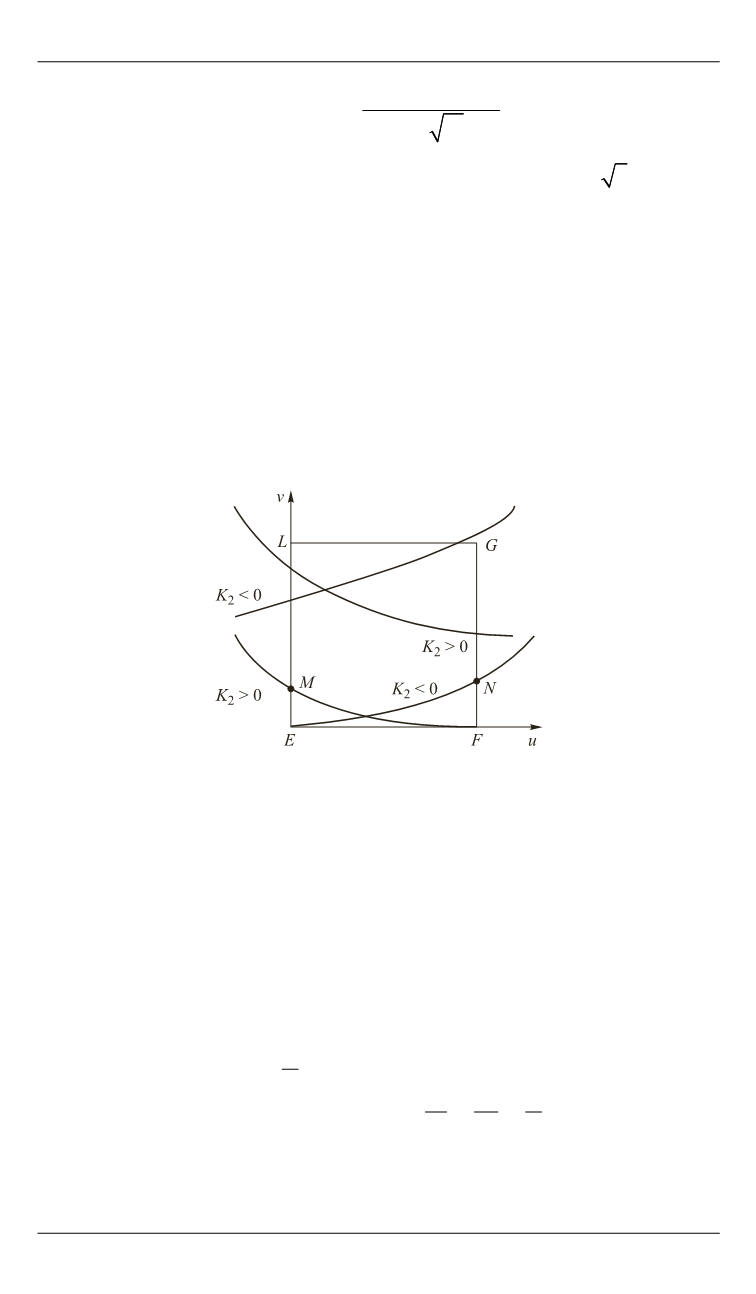
Э.Р. Смольяков
8
2
1
/ =
.
( / (2 } 1)
K
dv du
K v
(21)
Поскольку в любой экономической системе
1
2
K v
, то при
2
0
K
получаем
/
0
dv du
. Следовательно, в квадрате
EFGL
(ри-
сунок) при
2
0
K
уровни функции
1
H
имеют отрицательный
наклон, а при
2
0
K
— положительный, причем все эти уровни под-
ходят к оси
u
по касательной. Как видно на рисунке, чем выше уро-
вень
1
const
H
, тем большее значение принимает гамильтониан
1
H
и тем он предпочтительнее для 1-го игрока. Уровни функции
2
const
H
, очевидно, горизонтальны, причем для 2-го игрока пред-
почтительнее (см. рисунок) более высокие уровни (для случая
( ) 0
K t
).
Найдем все игровые равновесия в квадрате
EFGL
(см. рисунок)
для первой статической локальной игры, отвечающей случаю
2
> 0
K
,
т. е. на интервале времени
0
( , ').
t t
Прежде всего для первой локальной игры с платежными функция-
ми
1
( , )
H u v
и
2
( , )
H u v
найдем наиболее слабые
A
-равновесия в пря-
моугольнике
EFGL
(см. рисунок), под которыми на самом деле в этой
игре понимаем
c
A
-равновесия.
i
A
-экстремальные ситуации и
A
-
равновесие задаем следующими фигурами и отрезками:
1
2
= [
];
= [ ]; = [ ].
A FGLMF A GL A GL
Более сильные
B
- и
D
-равновесия на множестве
A
имеют вид
1
2
1
2
= [ ], = , = ; = = = .
B GL B G B G D D D G