А.А. Пожалостин, Д.А. Гончаров
6
2
0
0
1
4
i
i
i
r
r
J
R
∞
=
μ⎛ ⎞
= γ
+ β
⎜ ⎟
⎝ ⎠
∑
,
где
2
0
;
8
R
β =
2
2
0
4
( )
i
i
i
R
J
γ =
μ μ
.
Вводя обозначения:
0
0
,
i
i
γ
α =
β
2
2
,
i
i
H
R
μ
α =
2
( )
2
1
11
2
,
i
i
i
R
R
μ
α = − ρ ω
μ
2
2
( )
2
2
12
2
ch
,
i
i
i
R
H
R
μ⎛
⎞
α = ρ ω ⎜
⎟
μ ⎝
⎠
2
2
1
2
2
2
th
,
i
i
i
i
R
b
R
μ⎛ ⎞
=
α + ρ ω
⎜ ⎟
μ
⎝ ⎠
2
2
1
( )
2
12
( )
2
11
2
2
2
2
2
2
,
ch
th
i
i
i
i
i
i
i
i
R
b
R
R
ρ ω
α
μ
= α +
μ α ⎛ ⎞ α − ρ ω
⎜ ⎟
μ
⎝ ⎠
( )
12
1
0
2 2
1
ch
i
i
i
i
i
b
⎡
α ⎤
β = α −⎢
⎥ α ⎣
⎦
,
( )
2
0
12
2
2
1
2
2 2
2
2 2
1 1
1
,
ch
ch
i
i
i
i
i
i
i
i
i
R
b b
b
⎡
⎤
α
⎡
α ⎤
β =
+ ρ ω −
⎢
⎥
⎢
⎥
α
μ
α ⎣
⎦
⎣
⎦
представим частотное уравнение в виде
2
2
0
2
2
2
0
2
1
1
0
2
2
0
1
1
1
( )
( )ch
( )
.
i
i
i
i
i
i
i
i
i
i
i
i
i
R
R
J
J
J
∞
∞
∞
=
=
=
⎡
⎤
γ μ
ω ρ β
μ α − ρ β
μ Λ =
⎢
⎥
μ
μ
β
⎣
⎦
∑
∑
∑
(14)
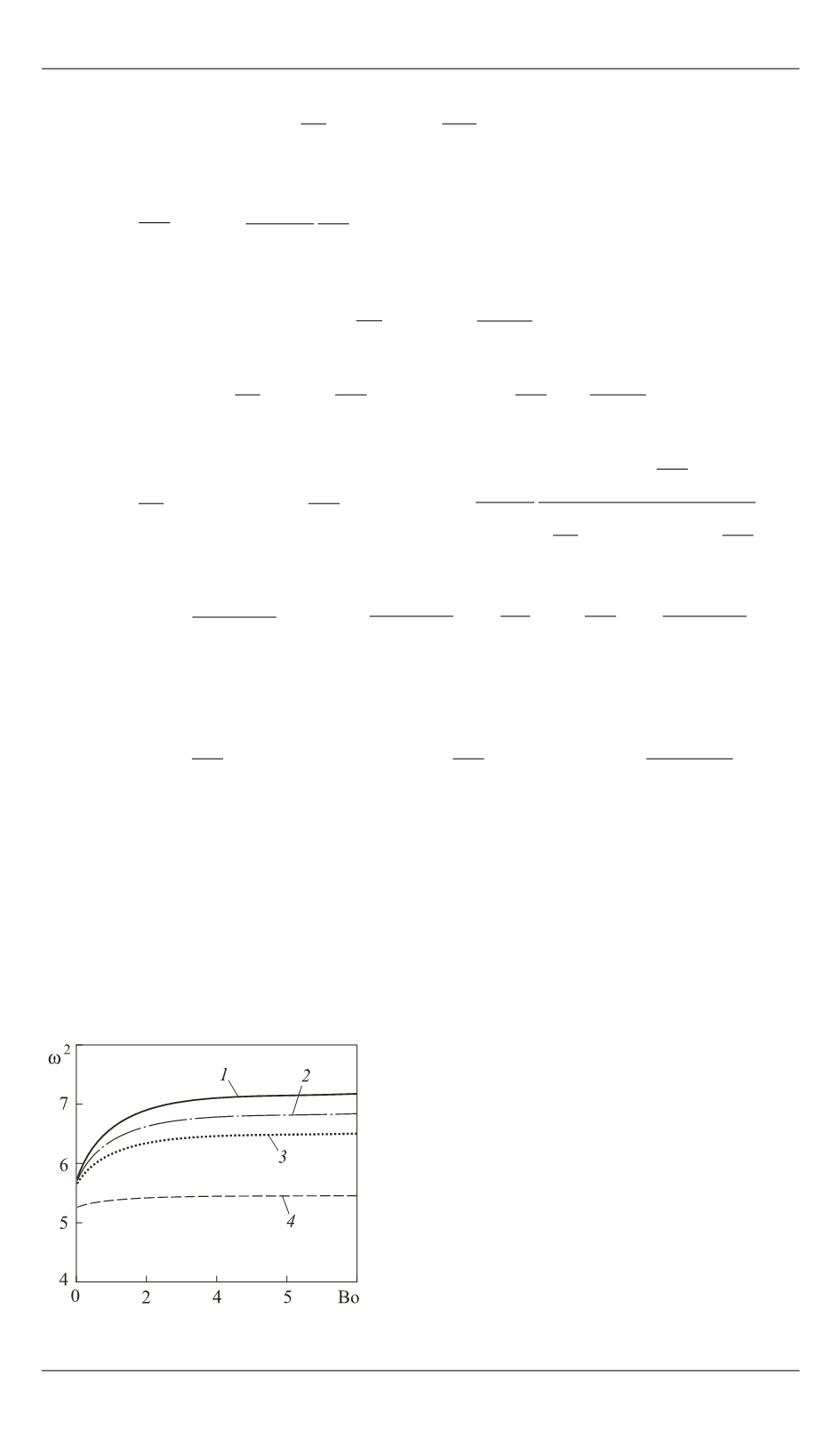
Ограничим сумму ряда (14) пятью членами и получим зависимость
квадрата собственной частоты первого тона колебаний
2
ω
от числа
Бонда Bo (рис. 2). При построении зависимостей принимали:
30 кг,
S
m
=
2
70
ρ =
кг/м
3
,
1
2
0,9 ,
ρ = ρ
1
R
=
м,
1
1
h
=
м,
2
1
h
=
м. Из
условия Bo = 0 находим значение критической частоты, которая свиде-
тельствует об отсутствии нарушения односвязности объема жидкости.
Рис. 2.
Зависимость квадрата
собственной частоты
2
ω
от чис-
ла Бонда Bo при
τ
= 2 000 Н/м,
кр
ω =
2,39 с
–1
(
1
),
τ
= 1500 Н/м,
кр
ω =
2,26 с
–1
(
2
),
τ
= 1800 Н/м,
кр
ω =
2,37 с
–1
(
3
),
τ
= 1900 Н/м,
кр
ω =
2,38 с
–1
(
4
)


