А.А. Пожалостин, Д.А. Гончаров
2
тах [8, 9] получены приближенные аналитические решения задачи без
учета и с учетом сил поверхностного натяжения. В работе [10] рассмот-
рена устойчивость малых колебаний свободной поверхности жидкости
в жесткой цилиндрической оболочке. В работе [11] приведены исследо-
вания колебаний многослойных жидкостей совместно с разделяющими
мембранами; получено приближенное решение, согласуемое с прове-
денным в [8].
Исследуемую краевую задачу можно рассматривать в качестве
модельной для анализа динамики разгонного блока ракеты-носителя
на пассивном участке траектории.
Постановка задачи.
Для получения точного аналитического ре-
шения краевой задачи сделаем следующие допущения:
1) жидкость заполняет цилиндрический бак с плоским упругим
разделителем, закрытый жестким плоским днищем;
2) материал мембраны однородный, изотропный и подчиняется за-
кону Гука;
3) жидкость идеальная, несжи-
маемая, ее движение — потенциаль-
ное, с потенциалом скоростей
.
Φ
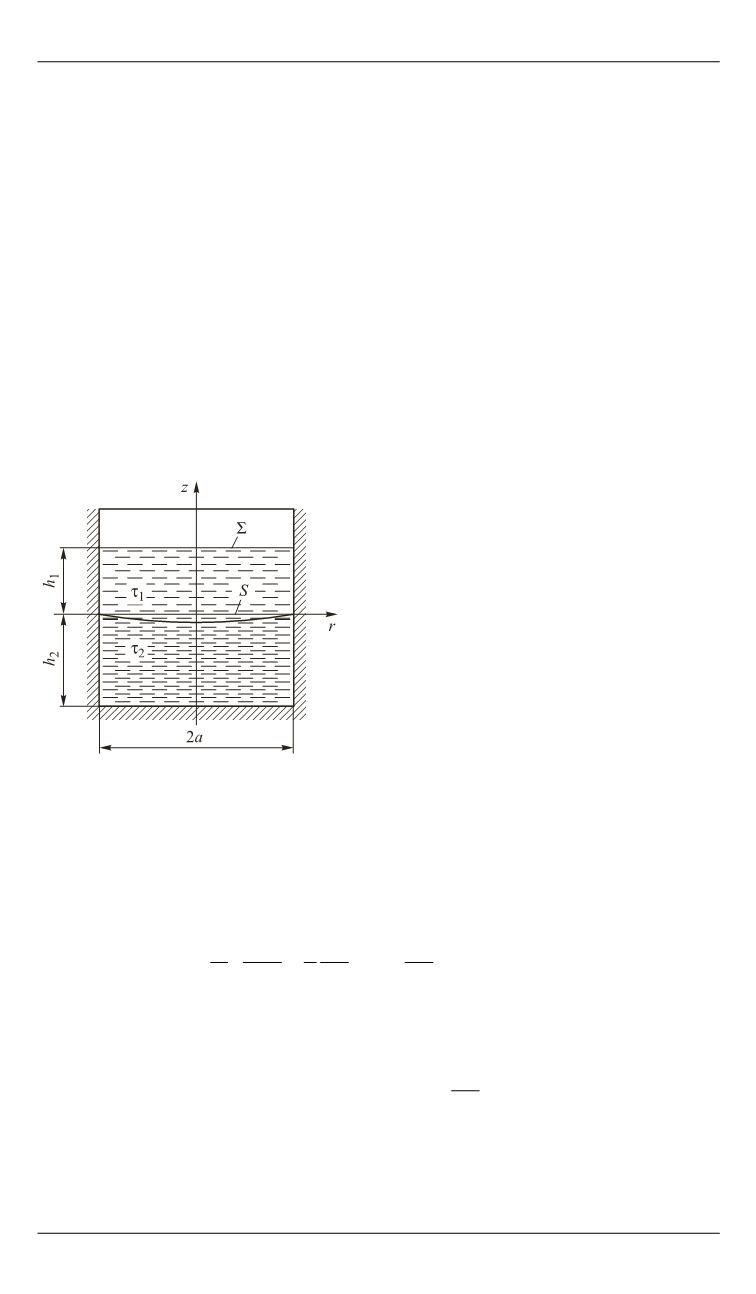
Рассмотрим нормальные колеба-
ния жидкости (рис. 1). Потенциал
скоростей должен удовлетворять
уравнению Лапласа
2
0
∇ Φ =
в обла-
сти
τ
(
τ
— объем, занимаемый
жидкостью). Слой
1
жидкости плот-
ностью
1
ρ
занимает полость объе-
мом
1
τ
и высотой
1
h
, а слой
2
плот-
ностью
2
ρ
— полость объемом
2
τ
и
высотой
2
h
. Невозмущенную поверхность жидкости обозначим как
Σ
, невозмущенную поверхность мембраны — как
.
S
Уравнение
движения упругого разделителя с граничным условием имеет вид
2
0
2
1
1
( , ),
w w w p r t
T r r r
t
∂
∂
∂
⎛
⎞
+ + ρ δ = −
⎜
⎟
∂
∂
∂
⎝
⎠
( , ) 0
w r t
=
при
.
r R
=
Здесь
w
— перемещение мембраны;
;
w w
t
∂
=
∂
0
ρ
,
δ
,
Т
— плотность
материала, толщина и натяжение мембраны соответственно;
p
– гид-
родинамическое давление жидкости на мембрану;
R
— радиус ци-
линдра. В дальнейшем инерцией мембраны пренебрегаем.
Рис. 1.
Модель бака, заполненно-
го жидкостью с разделителем


