О реализации еще одной возможности повышения устойчивости движения автомобиля
5
При положительных значениях (в определенных пределах) коэф-
фициента
cc
получаем передаточную функцию и, соответственно,
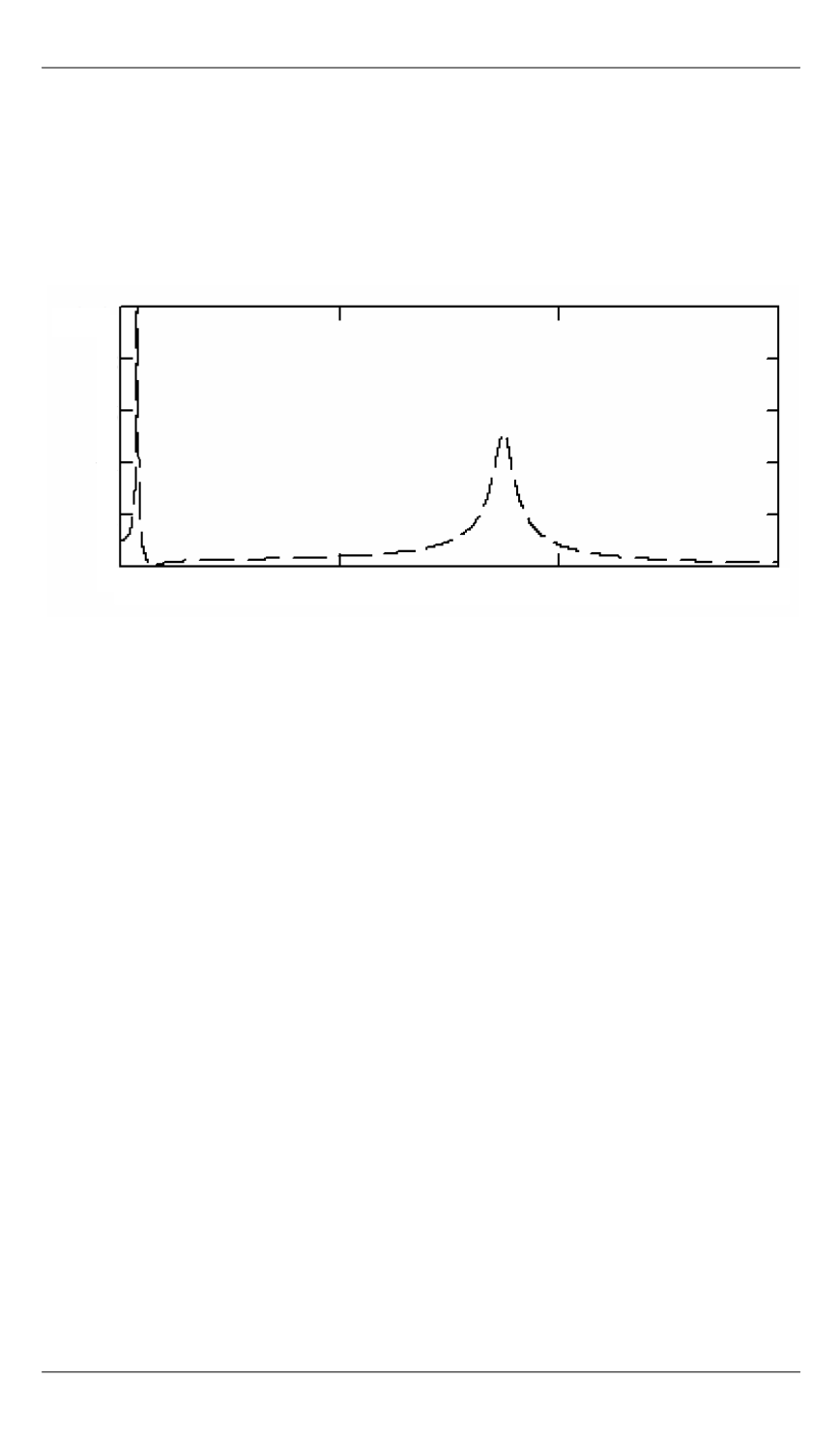
амплитудно-частотную характеристику колебаний подрессоренной
массы системы подрессоривания с управлением при кинематическом
возбуждении (рис. 3).
А ( )
ω
8
6
4
2
0
50
100
, рад/с
ω
Рис. 3.
Амплитудно-частотная характеристика колебаний неподрессоренной
массы системы подрессоривания с управлением при кинематическом
возбуждении
Сравнивая диаграммы на рис. 2 и 3, видим, что при введении
управления вертикальными реакциями дороги на колесо, резонансная
частота колеса сдвигается в область бóльших значений. При этом в
области резонансной частоты неподрессоренных масс пассивной си-
стемы подрессоривания, т.
е. системы без управления реакциями до-
роги на колесо, амплитуда колебаний колес в системе подрессорива-
ния с управлением резко уменьшается, в приведенном случае при-
мерно в 30 раз. Приведенная задача анализа колебаний в системе с
управлением была рассмотрена в линейной постановке.
При движении автомобиля в режиме резонанса колес может воз-
никнуть их отрыв от дороги. В этом случае функция связи колеса с
дорогой принимает нелинейный характер. К описанию, принятому
для линейной модели, добавляется условие, заключающееся в том,
что вертикальная реакция колеса
0,
z
R
≥
т.
е. она не может быть от-
рицательной.
Для решения такой нелинейной задачи применим метод имита-
ционного моделирования, это позволило воспользоваться пакетом
Matlab Simulink. Модель системы подрессоривания с управлением
вертикальными реакциями при движении по периодическому профи-
лю, выполненная в этом пакете, показана на рис. 4.


