В.В. Ларин
6
(
)
3/4
ном
ном
0,1
1 10
4
z
z
w
w
z
w
w
k P p
p
h
p
p
′
+
=
+
,
где
z
k
′
— коэффициент, постоянный для данной шины,
3/4
м МПа/Н .
⋅
Как видно на рис. 2, относительные погрешности при расчете по
формуле (4) достаточно стабильны и незначительны (не более 10 %)
во всех диапазонах изменения
w
p
и
z
P
.
Имея приемлемые выражения для определения
ш в
f
и
z
h
, можно
переходить к более сложным моделям, описывающим взаимодей-
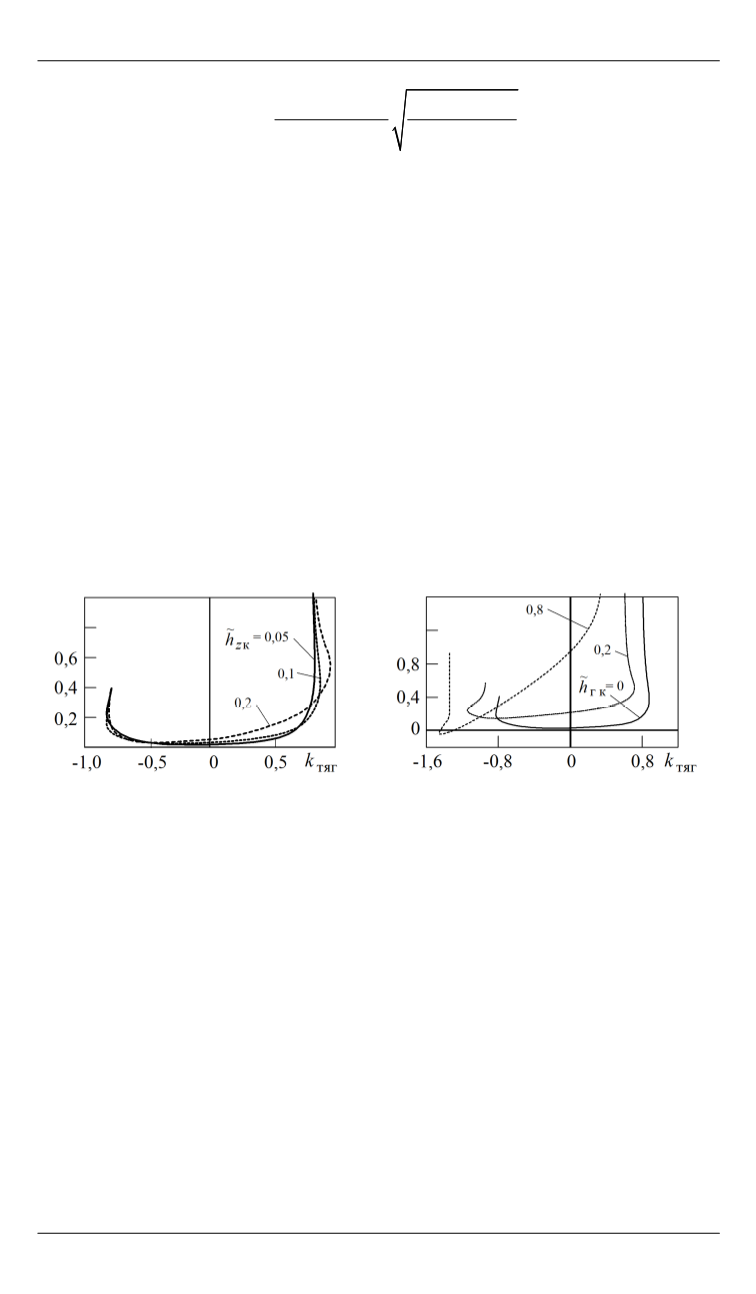
ствие КД с ОП. Представленные на рис. 3 расчетные зависимости ко-
эффициента мощности сопротивления качению
f
N
f
от коэффициен-
та тяги
тяг
/
x z
k P P
=
учитывают распределение нормальных и каса-
тельных напряжений по длине контакта шины с ОП. Для твердой ОП
кривые построены при различной относительной деформации колеса
к
св
/
z
z
h h r
=
%
(см. рис. 3,
а
) [5], а для деформируемой ОП — от относи-
тельной деформации грунта
г к г св
/
h h r
=
%
(см. рис. 3,
б
) [1].
а
б
fN
f
fN
f
Рис. 3.
Зависимости коэффициента мощности сопротивления качению КД с
шиной 1600×600-685 при
75
z
P
=
кН от коэффициента тяги и относительной
деформации колеса на твердой ОП (
а
) и на деформируемой ОП грунта (
б
)
Таким образом, предлагаемые зависимости позволяют повысить
точность расчета
ш в
f
КД при изменяемых значениях эксплуатаци-
онных параметров
z
P
и
w
p
, а тем самым параметров подвижности и
загруженности систем КТС.
ЛИТЕРАТУРА
[1] Ларин В.В.
Теория движения полноприводных колесных машин
. Москва,
Изд-во МГТУ им. Н.Э. Баумана, 2010, 391 с.
[2] Агейкин Я.С.
Проходимость автомобилей
. Москва, Машиностроение,
1981, 232 с.


