Задача оптимального управления параметрами амортизационных стоек самолета при взлете и посадке - page 3

Задача оптимального управления параметрами амортизационных стоек самолета…
3
Систему уравнений, которая описывает движение самолета в
плоскости g g x Oy , можно представить в следующем виде [4]:
   
 
3
ц.т ст
1
3 3
a ст ст ст
1 1
3
ц. т a ст
1
;
;
.
g y a j
j
z z j j j j y j
j j
g x j j
j
my G Y R
I M R x f R L Тh
m x T G X f R

 

  
    
   

 




Здесь и далее обозначено: ц.т ;
g y y  ц. т ;
g y y    ц. т ;
g y y    ц. т ;
g x x 
ц. т ;
g x x    ц. т .
g x x   
В эту систему уравнений входят следующие величины: Gx =
sin mg   — сила тяжести, спроецированная на ось ;
g Ox Gy =
cos mg    — сила тяжести, спроецированная на ось g Oy ; Т — сум-
марная тяга маршевых двигателей летательного аппарата; j f — ко-
эффициент сопротивления j-го колеса при касании опорной поверх-
ности; ст ,
j y j x L — координаты колесного шасси относительно цен-
тра масс самолета в связанной системе координат (см. рис. 1);
1, 2, 3 j  — номер амортизационной стойки.
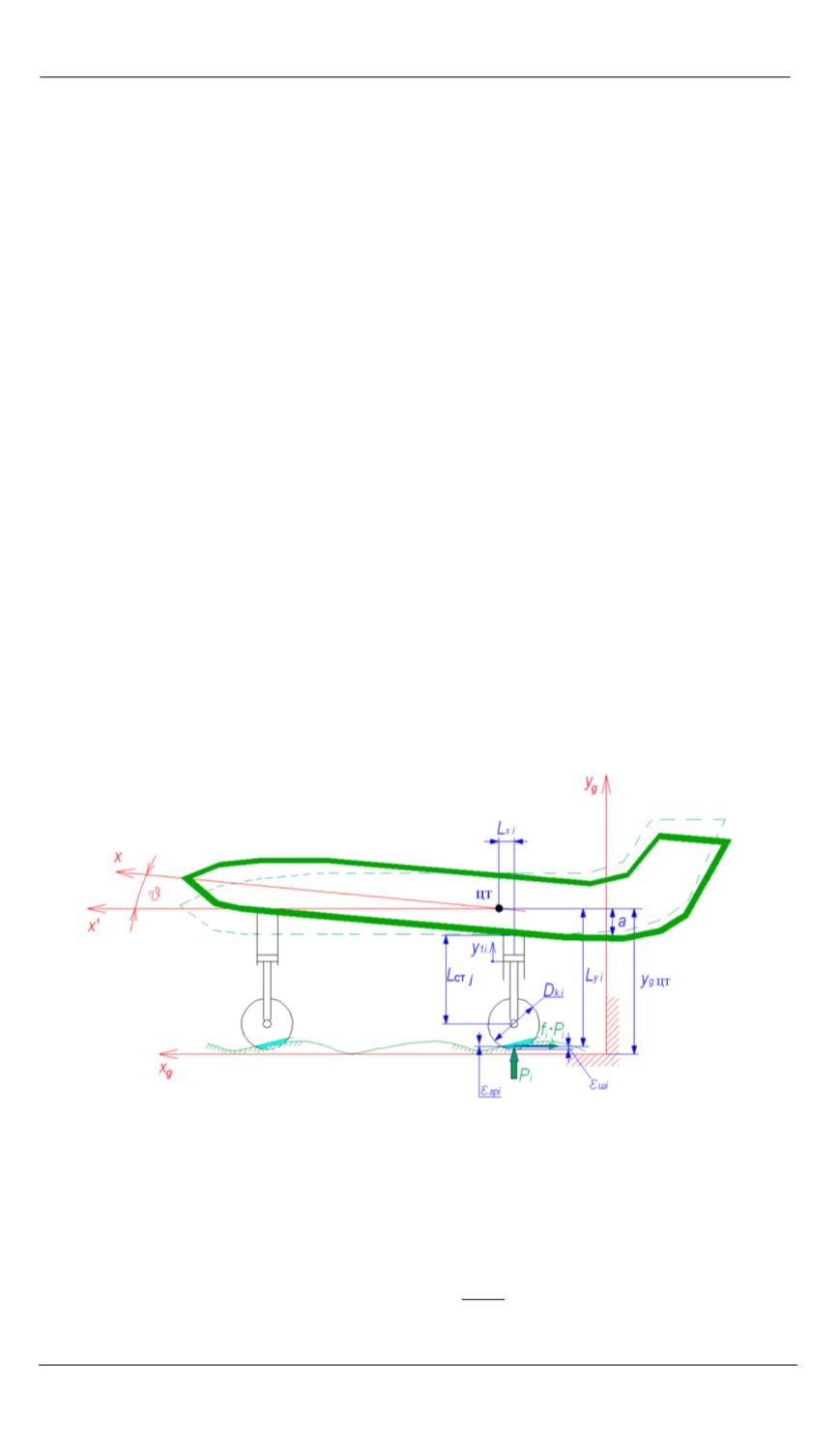
Рис. 1. Расчетная схема движения самолета по ВПП с неровностями
Перемещение штока гидроцилиндра j-й стойки уст j можно задать
через перемещение центра тяжести самолета, профиль неровности, а
также обжатие грунта и самого колеса шасси (см. рис. 1):
к
ст ст 0 ст гр ш пр sin .
2
j
j j j j j j
D
y a L y x y          