А.Ф. Грибов, Е.Н. Жидков, И.К. Краснов
4
1 при
0;0,5 ;
5 при
0,5;1 .
x
k x
x
Число интервалов дискретизации равно 20,
21,
N
0, 05.
h
Минимизация функционала как функции
1
N
переменной про-
водилась методом случайного поиска, основой которого является
итерационный процесс
1
,
0,1, ,
|
|
n
n
n
k
k
n
где
0
n
– величина шага;
2 3
( , , ,
)
N
– реализация
N
1-мер-
ного случайного вектора.
Начальное приближение
0
5,5, ,5 .
k
Число неудачных попы-
ток на очередном шаге найти меньшее значение минимизируемой
функции
max
3 .
N
N
В случае если все попытки были неудачными, шаг поиска
уменьшался, и процедура повторялась до
4
10 .
Результаты расче-
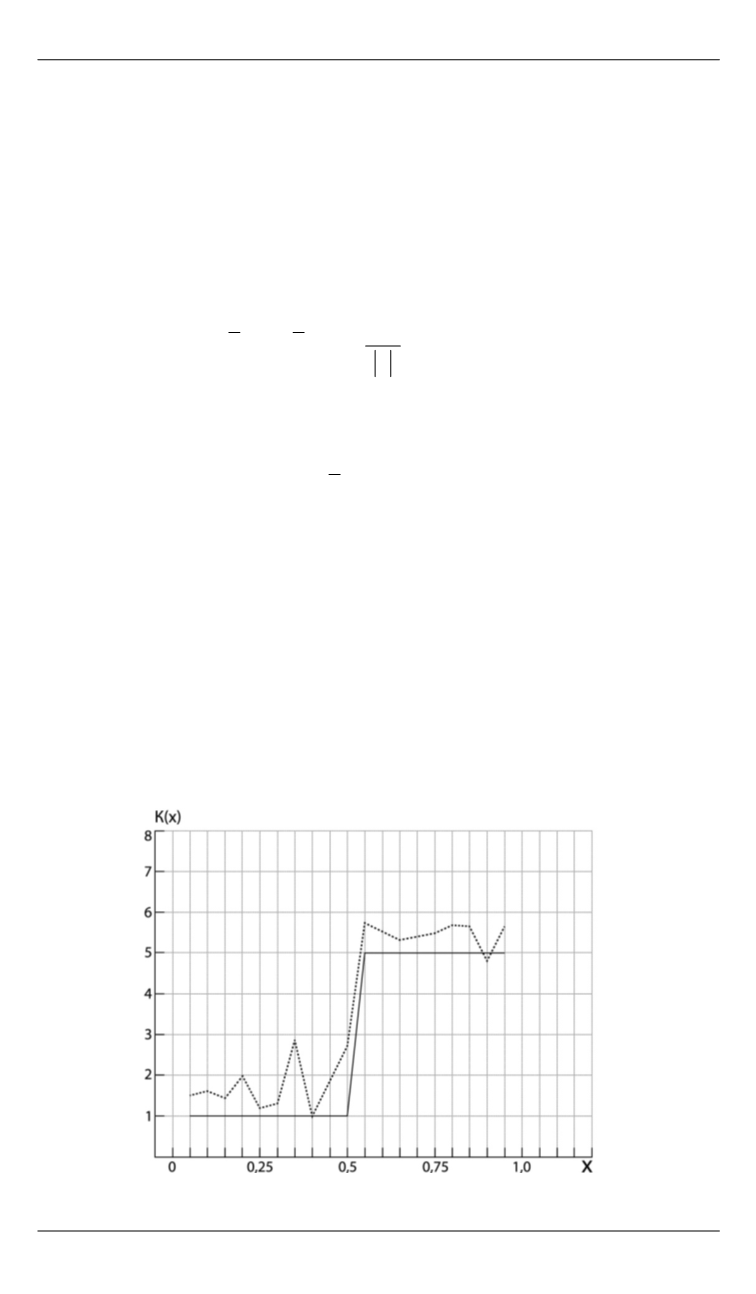
тов приведены на рис. 1 и 2. На рис. 1 сплошной линией показаны
значения коэффициентов
( )
k x
при решении прямой задачи, пункти-
ром – результат решения обратной задачи. На рис. 2 показаны ре-
зультаты решения прямой и обратной задач при
T
= 2. Сплошная
кривая – решение прямой задачи, пунктирная – восстановленное рас-
пределение температуры.
Рис. 1.
Коэффициенты
k
(
x
): —— – точные; ········· – восстановленные


