Моделирование процесса ползучести конструкционных материалов
3
Трехэлементная модель упругопла-
стического элемента и кривая ползучести
материала.
Точнее описать поведение ма-
териала под нагрузкой можно при помощи
более сложных сочетаниях упругих и пла-
стических элементов. Так, если соединить
два упругих и один пластический элемент,
причем упругие элементы соединить после-
довательно (рис. 5), получим следующую
систему уравнений, описывающих процесс
деформирования материала:
y2
п п
п y2
y1
1 y1 y1
y1 y2
2 y2
y2
,
,
,
,
,
,
K
E
E
(5)
где σ
у1
,
E
1
,
ε
у1
– напряжение, модуль упругости и деформация 1-го
упругого элемента; σ
у2
,
E
2
,
ε
у2
– напряжение, модуль упругости и де-
формации 2-го упругого элемента.
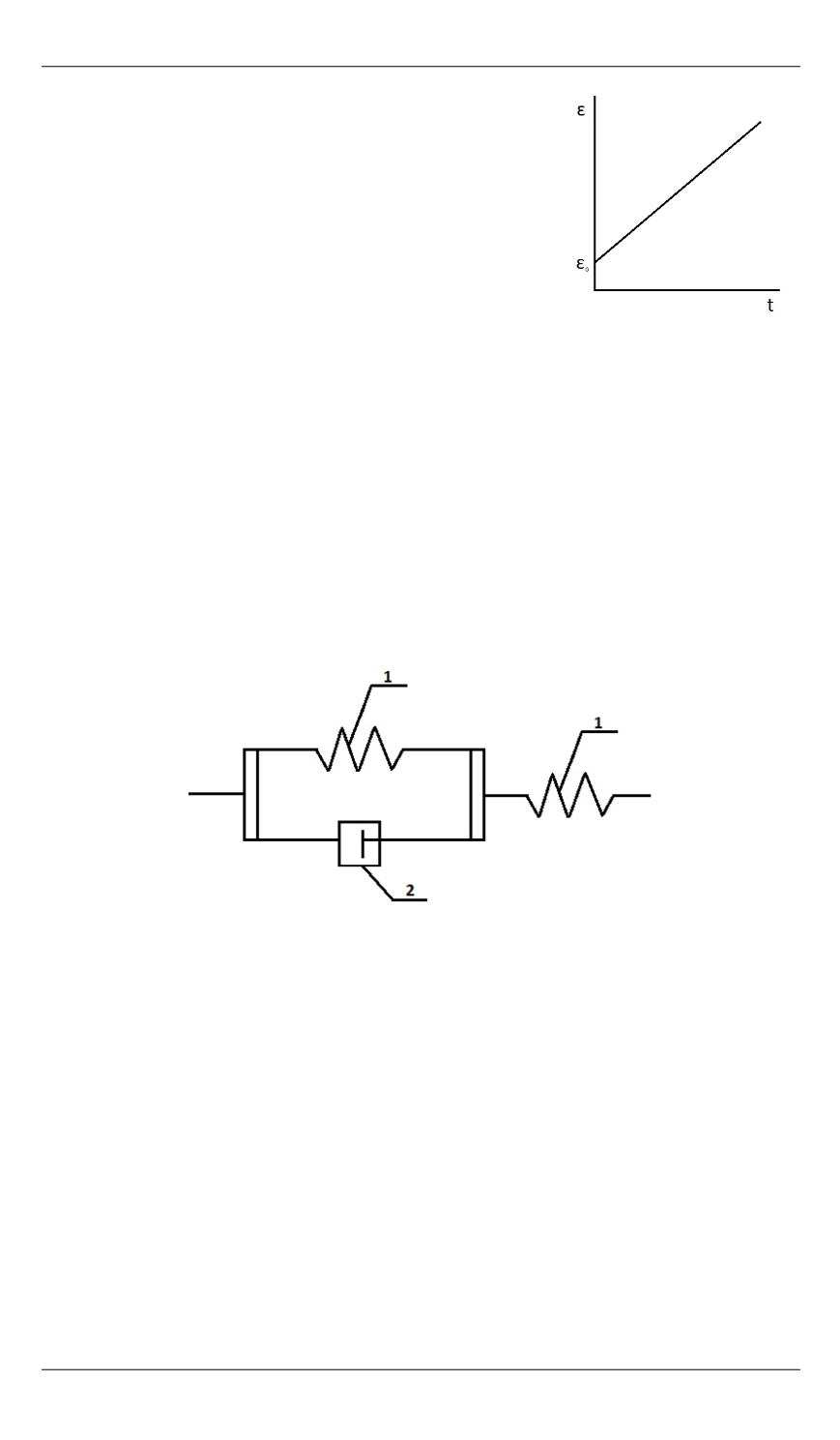
Рис. 5.
Трехэлементная модель с последовательным соединением элементов:
1
– упругий элемент;
2
– пластический элемент
Исключив из (5) напряжения и деформации, относящиеся к от-
дельным элементам, получим закон деформирования модели
1
1 2
1 2
.
E K E E K E E
(6)
Если в трехэлементной модели упругие элементы соединить па-
раллельно (рис. 6), то получим следующую систему уравнений, опи-
сывающих процесс деформирования материала:
2
1 1 1
1
1
2 2 2
2
,
,
,
,
,
.
п
y
п
п y
y
y
y
п y
y
y
K
E
E
(7)
Рис. 4.
Деформация
ползучести для модели
Максвелла


